
When a city contemplates constructing a new highway or major roadway, it doesn’t simply break ground and start paving. Instead, an extensive feasibility study is conducted to evaluate various aspects including environmental impacts, traffic patterns, and potential congestion relief or creation, for example, the US 277 Sonora Safety Route Study and the I-5 JBLM Corridor Study. These studies examine traffic patterns specific to the project area, identify existing bottlenecks, and analyse how the new infrastructure will impact the overall transportation network.
Similarly, understanding traffic patterns is fundamental to designing and operating networks, influencing decisions across all temporal and structural scales. This knowledge shapes everything from long-term, macro-level topology design to millisecond-level, micro-scale buffer allocation and tuning.
This post explores the characteristics of various traffic models using synthetic data and offers an overview of traffic patterns. We’ll generate and analyse time series data to highlight the fundamental properties of different traffic models. In a follow-up post, we will apply these insights to a practical example, examining how these traffic patterns affect the performance of Random Early Detection (RED) parameter tuning.
This is also a very high-level overview of the topic to provide a broader perspective. Think of it as a guided foothills tour, providing a view of the distant peaks. The climb to those distant peaks is left as an adventure for readers to explore in the future.
Statistical distributions
Statistical distribution properties are fundamental in characterizing network traffic behaviour. They describe the underlying probability distributions of various traffic attributes, such as packet inter-arrival times, packet sizes, flow durations, and traffic volumes.
Heavy-tailed distributions
These are probability distributions whose tails are not exponentially bounded. In network traffic, heavy-tailed distributions are often observed in phenomena like flow durations, and inter-arrival times.
- Examples include Pareto, Weibull (with shape parameter < 1), and log-normal distributions.
- They exhibit the property P(X>x)∼x−α as x→∞ where 0<α<2.
- Heavy-tailed distributions can lead to high variability and extreme events in network traffic.
An example of a heavy-tailed distribution is shown in Figure 1 where we can see an extreme event shown by a spike, and its statistical characteristics.
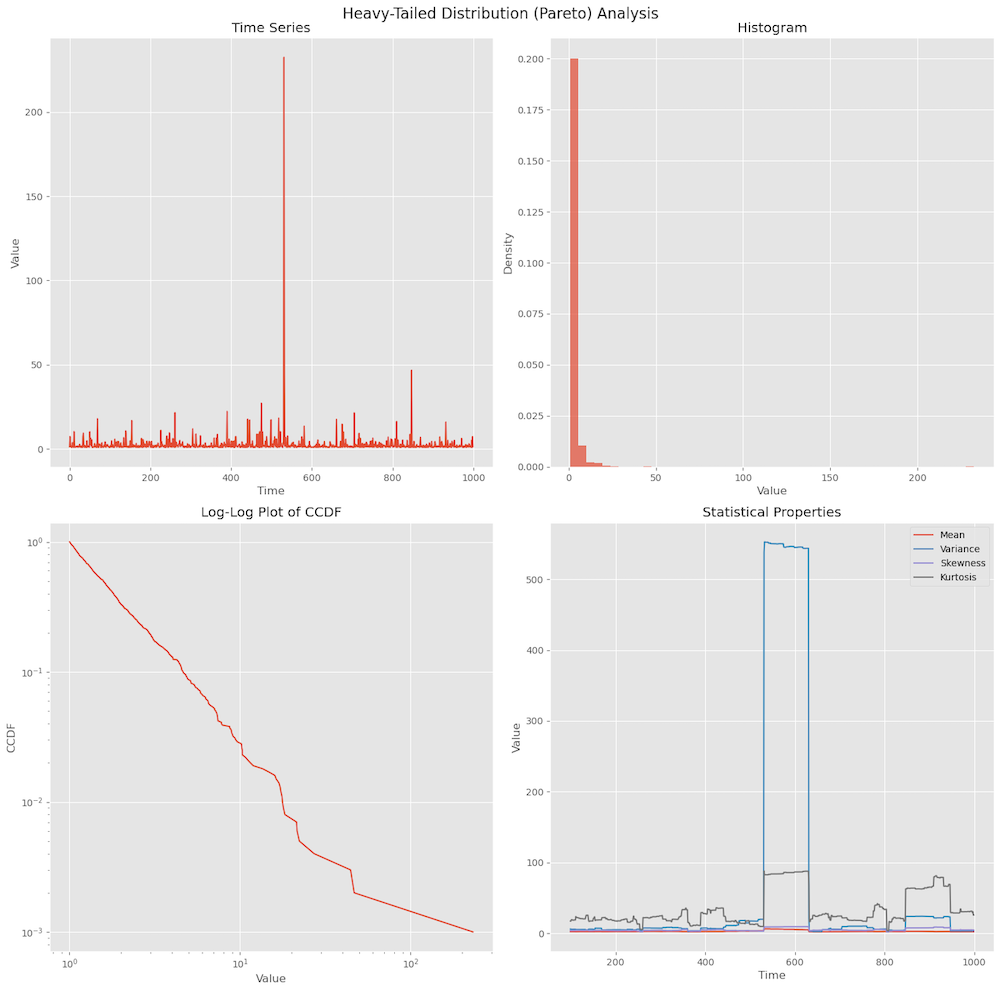
Service time distribution
This generally refers to the statistical distribution of packet sizes or the time required to process/transmit packets. Common models are exponential, deterministic, and more general phase-type distributions. The choice of service time distribution significantly affects queuing behaviour and network performance. Service times often exhibit multi-modal distributions due to different packet size classes (for example, ACKs, and MTU-sized packets). The service time distribution impacts the queueing behaviour — how packets accumulate in network queues.
Figure 2 shows an example of exponential distribution. In the time series plot, we can see many small values with occasional large spikes. The histogram shows peal near zero and a long, gradually decreasing tail to the right.
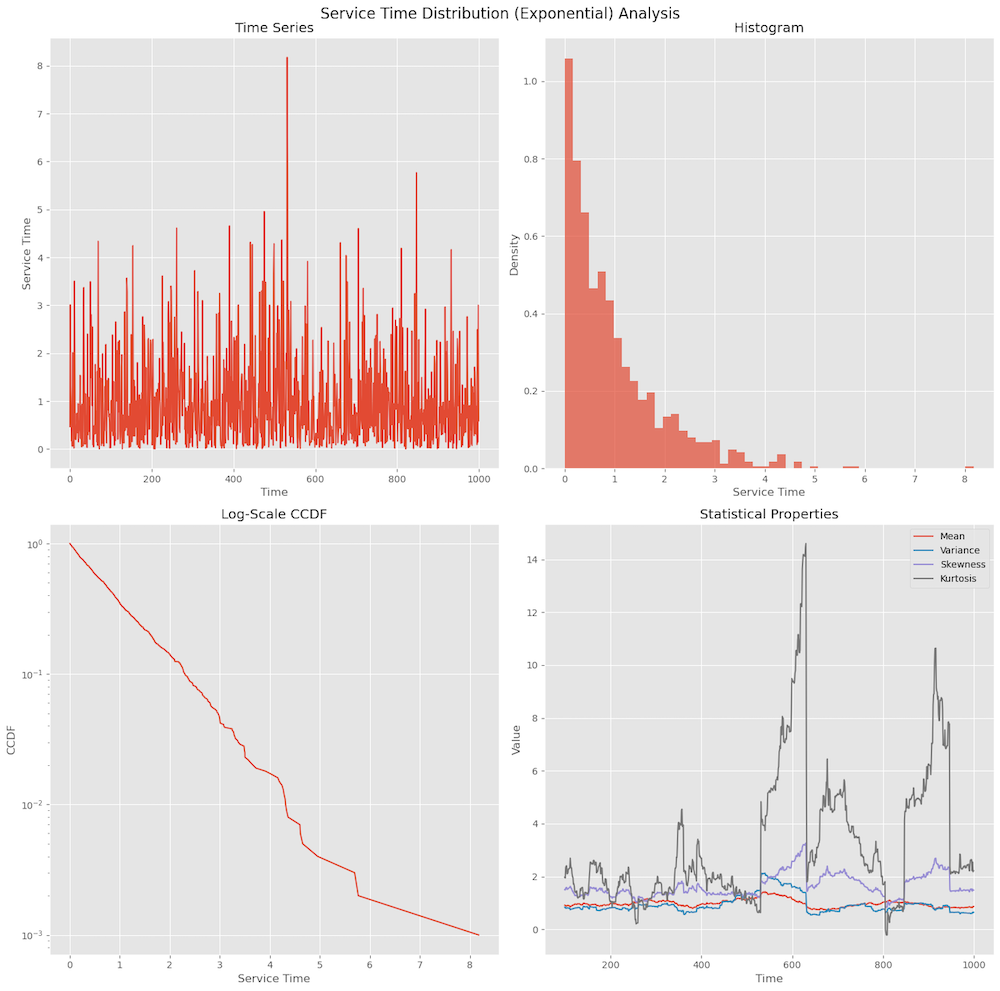
Arrival process
The arrival process describes the statistical nature of how packets or flows arrive at a network element. The arrival process can significantly impact on things like buffer occupation and packet loss.
Poisson process
The classic way was to use the Poisson process. It’s a stochastic process where events (packet arrivals) occur continuously and independently at a constant average rate. The inter-arrival times are exponentially distributed.
One of the key properties of the Poisson process is memorylessness. This means that the probability of an arrival occurring in the next time interval is independent of previous arrivals. The arrival rate λ is constant over time, which is a very naive assumption compared to how the real traffic behaves, and that is the reason it cannot capture burstiness or correlation in real network traffic.
Much of the earlier research used the Poisson arrival process as an assumption for packet arrival, but it’s a very simplistic view and the real traffic patterns are more complicated.
Batch Markovian Arrival Process (BMAP)
An extension of the Poisson process that allows for batch arrivals and captures correlations and burstiness in traffic. BMAP supports batch arrivals, meaning multiple packets can arrive simultaneously, and this process is governed by an underlying Markov chain. This is suitable for modelling traffic with correlated arrivals such as bursts of packets or flows.
Self-similar arrival processes
Arrival processes that exhibit self-similarity have statistical properties that remain consistent across different time scales. One key property is Long-Range Dependence (LRD), where significant correlations exist between arrivals even when separated by long time intervals. These processes also exhibit fractal behaviour, meaning the arrival process appears similar across various time scales. This fractal behaviour is evident in self-similar traffic, where zooming in from hours to seconds reveals the same patterns, unlike Poisson traffic.
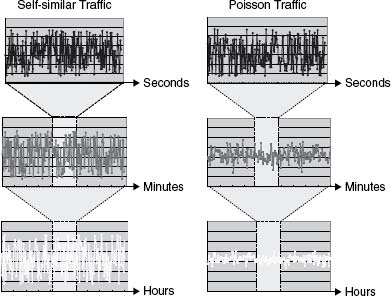
We can measure self-similarity using the Hurst parameter, where 0.5<H<1 indicates LRD. We will explore self-similarity and LRD further in a later section.
Markov Modulated Poisson Process (MMPP)
MMPP is a Poisson process where the arrival rate is governed by a Markov chain, allowing the rate to change based on different states. This allows us to model state-dependent arrival rates, where we can have different arrival rates for different states of the underlying Markov chain. This is suitable to model traffic with different modes such as high and low traffic periods.
Figure 4 shows various arrival processes and how they look different. Anytime you are modelling things like scheduling, buffer occupancy, and so on, the type of arrival process matters. This makes it extremely important on what assumptions one is making for the traffic pattern.
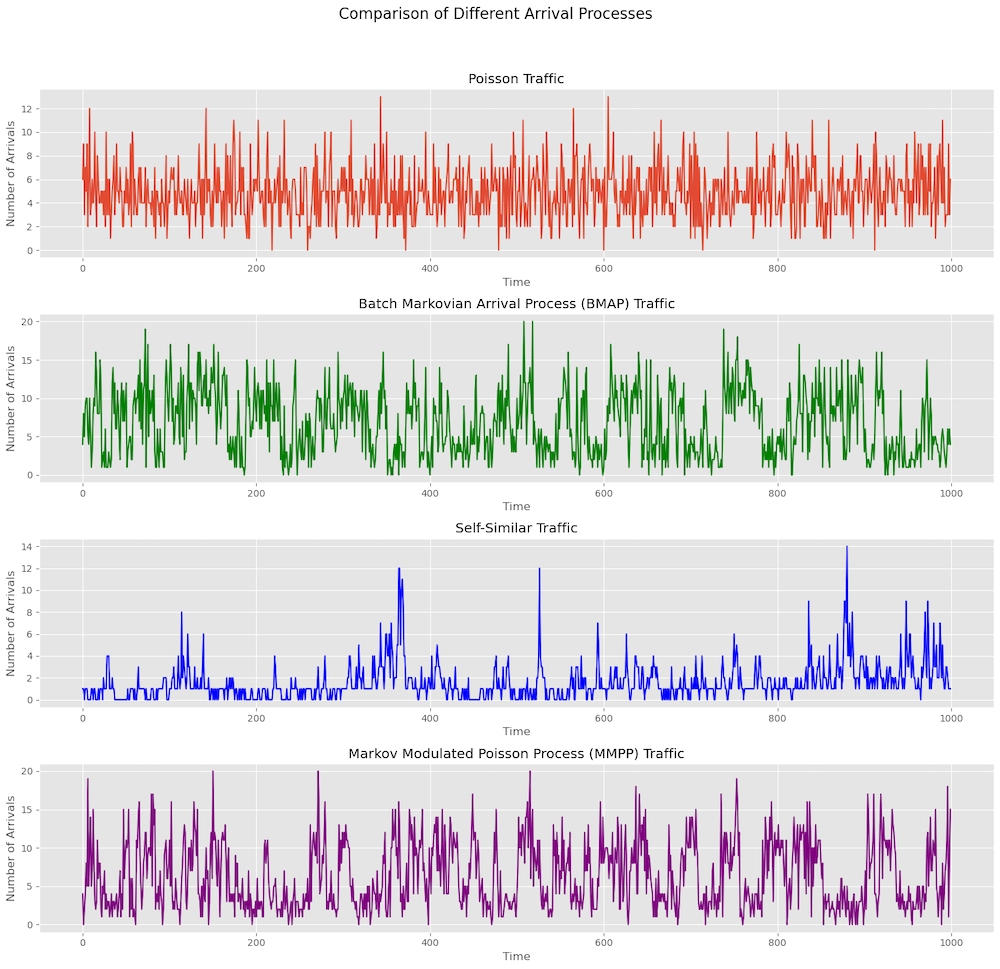
Temporal patterns
Seasonality and trend
Seasonality refers to regular and predictable patterns or fluctuations at specific intervals. Examples of seasonality include traffic peaking during business hours and dropping at night. Understanding seasonality helps in traffic forecasting and capacity planning.
Trend is a long-term increase or decreases over time. The trend indicates the general direction in which traffic patterns are moving, irrespective of short-term fluctuations or seasonal effects.
Network traffic can have both seasonality and trend present. One can use Seasonal Decomposition of Time Series (STL) to decompose into seasonal, trend, and residual components. Seasonal Auto-Regressive Integrated Moving Average (SARIMA) is another classical model from econometrics that captures seasonality with Autoregressive Integrated Moving Average (ARIMA).
To extract the trend one can apply techniques like linear regression, moving average, exponential smoothing or Locally Weighted Polynomial Regression (LOESS). Figure 5 shows a time series that includes both seasonality and trend.
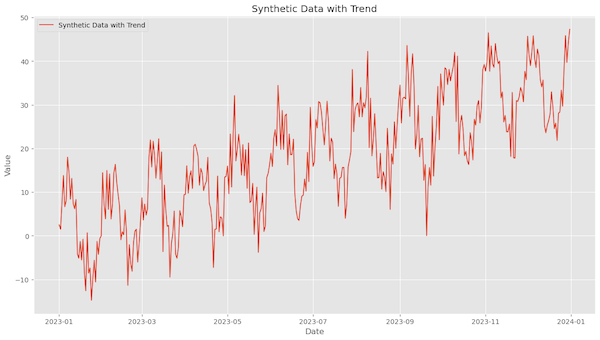
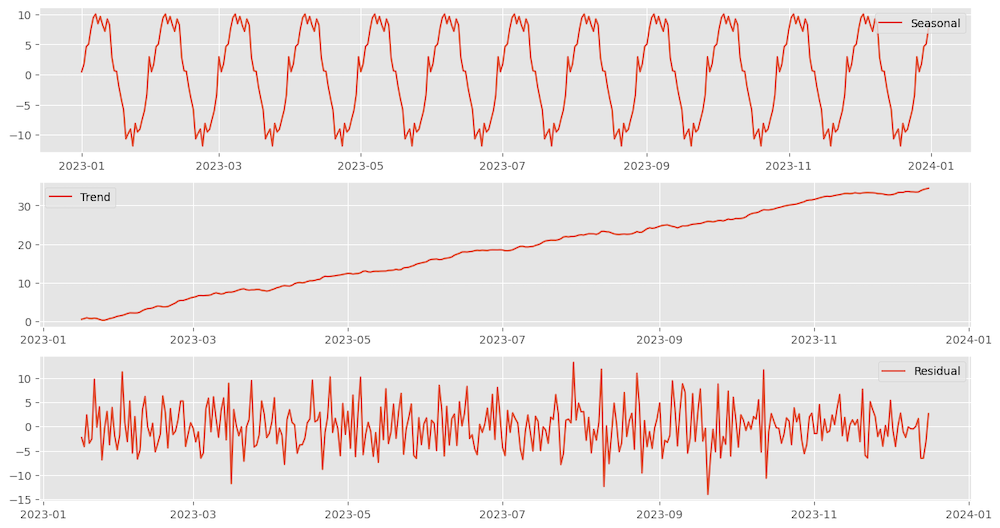
Decomposing Figure 5’s time series into seasonal, trend, and rest left as residual using STL is shown in Figure 6.
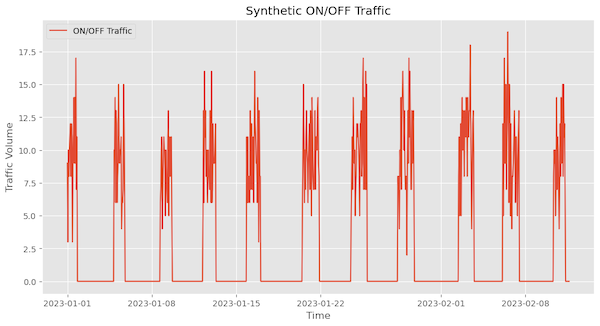
ON/OFF behaviour in network traffic
This refers to traffic patterns characterized by alternating periods of high activity (ON) and low or no activity (OFF). There is a burst of traffic during the ON periods, whereas, during the OFF periods, the traffic is minimal or nonexistent. An example of this would be traffic patterns between GPUs.
To characterize this behaviour, we must understand the duration of ON and OFF periods for burstiness analysis. This can be simulated using Markov-modulated processes and decomposed using Wavelet analysis.
Figure 7 shows synthetic traffic with an ON/OFF traffic pattern.
Scale-related properties
Scale-related properties focus on how traffic patterns behave and maintain consistency across different time scales.
Self-similarity and LRD
We already looked at this in the self-similar process section and as mentioned earlier, it’s a property where traffic patterns look similar across different time scales. This means that zooming in or out on the traffic data reveals similar structures and patterns, regardless of the time scale used.
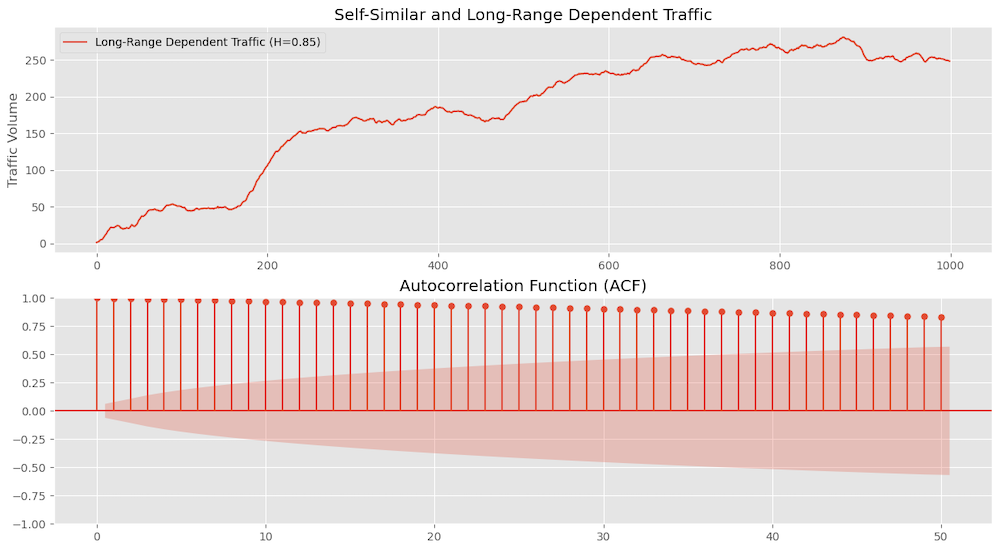
It can be measured by Hurst Parameter, which is a measure of self-similarity. Values of H range between 0.5 and 1.
- H = 0.5: indicates no long-term memory.
- 0.5<H<1: indicates self-similarity.
- H = 1: indicates perfect self-similarity.
LRD refers to significant correlations between values over long periods. We can measure this by looking at the Autocorrelation Function (ACF) plots to see the correlation.
Figure 8 shows synthetic traffic with ACF plots, which shows the values decay very slowly for the lags indicating strong correlation over long periods confirming LRD.
Multifractal scaling
This is a property where traffic exhibits different scaling behaviours at different moments. This implies that the statistical properties of the traffic can vary widely, depending on the timescale and the location in the time series.
We can use Multifractal Detrended Fluctuation Analysis (MFDFA) to measure the multifractal properties of time series data.
Variability and burstiness
Burstiness
This refers to high variability in traffic over short periods. It is characterized by sudden spikes or bursts in traffic volume.
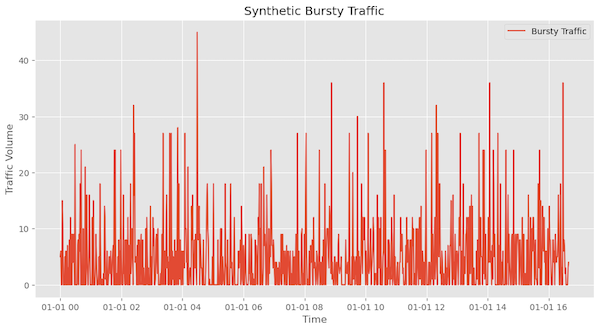
Peak-to-mean ratio
This is the difference between the peak and the average traffic rate over a period. This ratio is an important metric for understanding the extremes in traffic behaviour. Figure 10 is a histogram of Figure 9’s traffic highlighting the peak and average rate of traffic observed.
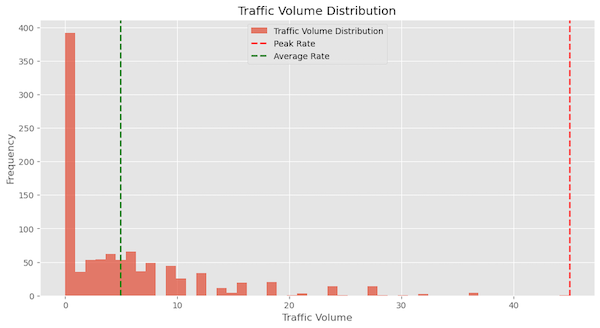
Variability (Coefficient of Variation)
The Coefficient of Variation (CV) is a measure of relative variability. It is defined as the ratio of the standard deviation to the mean of the traffic volume.
Correlation and dependency
Autocorrelation and partial autocorrelation
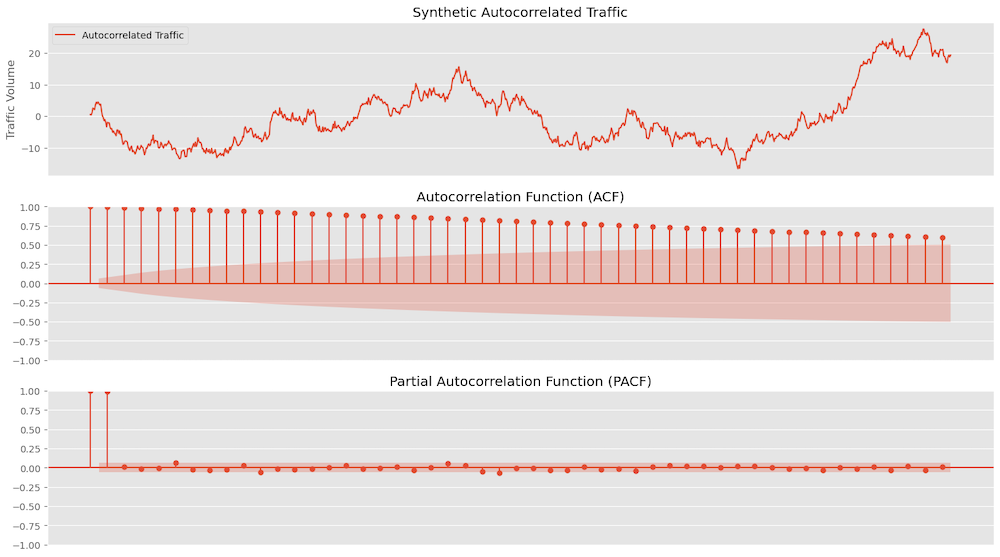
Autocorrelation is the correlation of a signal with a delayed copy of itself as a function of delay. In other words, it measures how similar the observations are between time series points separated by a given time lag. The autocorrelation function (ACF) gives us the correlation between any two values of the same variable at times ti and tj. We can also use PACF to measure the correlation between an observation Yt and Yt−k after removing the effects of all the intermediate observations Yt−1,Yt−2,…,Yt−k+1.
Figure 11 shows an auto-correlated series and the ACF plot shows that values start at 1 for lag 0 and remain significantly positive for many lags indicating strong autocorrelation. The slow decay of the ACF values indicates that the traffic has a strong autocorrelation structure, meaning that traffic volumes at one time point are highly influenced by previous lags. The sharp decline in the PACF values after the first few lags indicates that the traffic is primarily influenced by the most recent past values. This suggests that while there is strong autocorrelation in the short term, the direct influence of traffic volumes diminishes quickly with increasing lag.
Random walk
A random walk is a stochastic process that describes a path consisting of a succession of random steps. It is a fundamental concept in probability and is used to model various phenomena in fields such as physics, finance, and network theory.
Some main properties are:
- The path is formed by a series of steps, where each step is determined by a random process.
- Each step is independent of the previous steps.
- The statistical properties of the steps do not change over time (stationarity).
Examples:
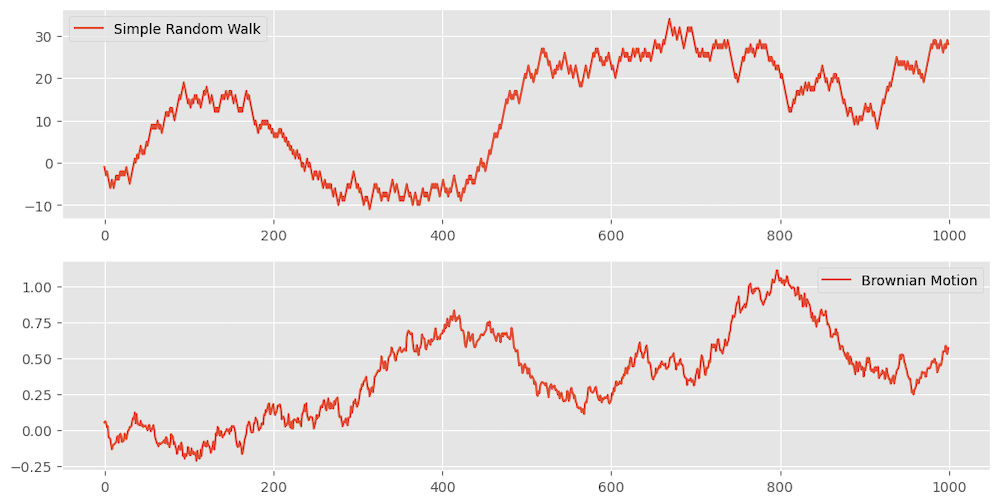
Simple random walk: A process where each step is equally likely to move up or down by a fixed amount. This can be given by Xt=Xt−1+ϵt. where ϵt is a random variable.
Brownian motion: A continuous-time random walk where the steps follow a normal distribution. This can be given by X(t)=X(0)+∫t0σdW(s) where W(s) is a Wiener process and σ is the volatility.
Figure 12 shows a synthetic simple random walk and Brownian motion example.
Stationarity and time-invariance
Stationarity
A time series is said to be stationary if its statistical properties, such as mean, variance, and autocorrelation, do not change over time. This implies that the process of generating the data remains constant over time.
Types of stationarity:
- Strict stationarity: The joint distribution of any set of observations is invariant under time shifts. This is a very strong condition and is rarely met in practice.
- Weak stationarity (second-order stationarity): Only the first two moments (mean and variance) and the autocorrelation structure are invariant under time shifts. This is more commonly used in practical applications.
A time series is said to be non-stationary if its statistical properties change over time. This includes changes in mean, variance, autocorrelation, and the presence of trends or seasonal patterns.
Figure 13 shows an example of a stationary time series, in which we can see the mean and variance seem to be stable over time.
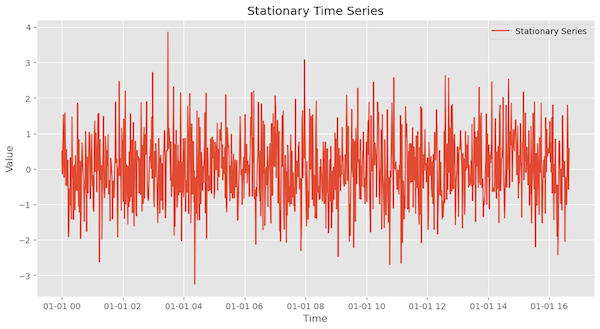
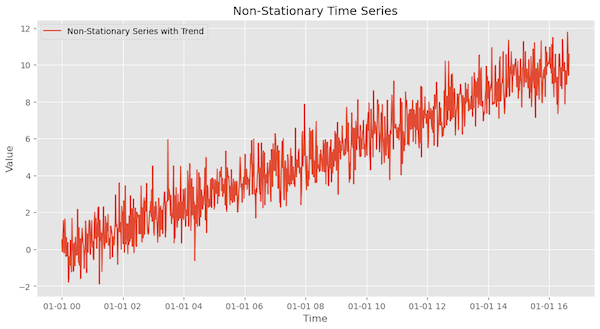
Figure 14 is an example of a non-stationary time series as it has a trend that means the mean is not constant over time.
Conclusion
We looked at several foundational properties of network traffic that are essential to understand. These include temporal patterns like seasonality and trends, scale-related behaviours such as self-similarity and LRD, and statistical distribution characteristics. Each property uniquely influences network performance. For example, buffer sizing and packet drops will vary depending on the traffic’s burstiness and arrival patterns.
In the next post, we will simulate a Random Early Detection (RED) process and explore how different parameters impact network performance based on various traffic characteristics.
Diptanshu Singh is a Network Engineer with extensive experience designing, implementing and operating large and complex customer networks.
Adapted from the original on Dip’s blog.
The views expressed by the authors of this blog are their own and do not necessarily reflect the views of APNIC. Please note a Code of Conduct applies to this blog.

I do keep hoping someone will show pie or codel behaviors. RED is dead.
Hey Dave, thanks for the suggestion. I haven’t explored PIE or CoDel in depth yet, but I’ll definitely add them to my to-do list. That said, in most data center environments, these mechanisms aren’t commonly implemented, which is why It hasn’t made into my priority list.
Does this approach make sense? From the largest Internet backbone: https://blog.arelion.com/2020/04/01/covid-19-network-trends-and-modelling/
The problem space falls into the TimeSeries Forecasting category; in that case, it uses a TimeSeries forecasting library called Prophet. Prophet is an additive model that uses piecewise linear/logistic trends; seasonality combines Fourier terms and a term to handle user-defined holidays, etc. It’s a good start, and definitely a good way to start bringing scientific rigor. I prefer ensemble methods where the forecast is a combination of various forecasting algorithms. https://otexts.com/fpp3/combinations.html
The problem space falls into the TimeSeries Forecasting category; in that case, it uses a TimeSeries forecasting library called Prophet. Prophet is an additive model that uses piecewise linear/logistic trends; seasonality combines Fourier terms and a term to handle user-defined holidays, etc. It’s a good start, and definitely a good way to start bringing scientific rigor. I prefer ensemble methods where the forecast is a combination of various forecasting algorithms. https://otexts.com/fpp3/combinations.html