
A chain is not as strong as its weakest link, it can be much much stronger than that. In cybersecurity, the art of building secure systems from insecure but diverse components is an important but often neglected topic; instead processes, rigidity, and structure are generally seen as the only way to attain security. This blog post examines how it is possible to attain secure systems or services through diversity.
This is the first in a series of blog posts on Security by diversity. Here we will focus on the scaling properties of reliability through diversity; later blog posts will introduce the business and economic aspects of security through diversity and discuss not only technical security but also how to secure coordination and similar organizational aspects.
Diversity
Technical diversity can be seen as a way of building systems or solutions from entities that are slightly different or independent from one another so as to increase security. The main benefit here is that diversity enables redundancy and avoids the serious consequences of having a single point of failure.
Another way to look at this issue is as Donald Rumsfeld phrased it in his infamous quote on the different categories of what is known:
Because as we know, there are known knowns; there are things we know we know. We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns—the ones we don’t know we don’t know […] it is the latter category that tends to be the difficult ones.
Donald Rumsfeld, US Department of Defence Briefing, 12 February 2002.
With diversity, we can essentially remove the probability of known knowns to interrupt a system, and can likely reduce the effects of known unknowns and unknown unknowns to such a degree that the system can withstand them.
Diverse entities differ in some important way; they could be in different geographical locations, connected with separate strands of fibre, built by different materials, and so on. Perhaps it is easier to illustrate a diverse system from another perspective; a diverse system is not the same everywhere, which means it has fewer single points of failure.
The mathematics of security by diversity
While terms like ‘diversity’ and ‘robustness’ frequently occur in security-related discussions, they are less frequently supported by the relevant data or analysis. In this section, my goal is to discuss robustness by calculating the probabilities of failure in diverse systems.
Before we start, I should introduce some essential terminology I will use below:
- Mean Time Between Failures (MTBF) is the average period of time that a system is functioning between failures. It does not include the time period of the failure itself.
- Mean Time to Recovery (MTTR) describes the average time it takes for a system to get back up after going down.
I will refer to a system as a set of nodes that together provide a service. If a system is not redundant, the failure of one node results in a failure of the system. A redundant system can handle loss of (some) nodes without loss of service.
Below, in Equation 1, I show the equation for calculating the probability of a service being up (Pₛ) given the total number of nodes (n), the number of nodes required to provide the service (m), and the probability that an individual node is up (Pₙ). The probability that an individual node is up (Pₙ) is calculated from MTBF and MTTR as Pₙ = MTBF / (MTBF + MTTR), and for these constructed examples MTBF and MTTR for nodes are assumed rather than calculated from prior data. In essence, the formula calculates the probability that at least the required number of nodes are up.
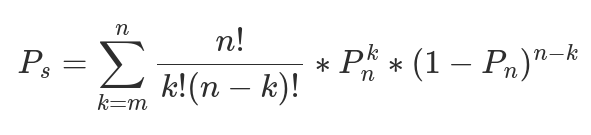
This is an idealized equation for system uptime derived from identical but otherwise independent nodes. That is, a calculation based on the known knowns. Completely independent and diverse nodes is the goal, but for practical purposes such independence is often impossible to achieve.
Two illustrative examples
The following section contains two examples of security by diversity. The first example (in Table 1) illustrates how well security by diversity scales, and the second example (in Table 2) is a real world example of a situation where the security by diversity solution is orders of magnitude better than other security measures.
| Per node | At system level | ||||
| MTTR | MTBF | Probability up | m/n | MTTR + MTBF | Probability up |
| 1h | 19h | 95.00% | 2-Feb | ~ 10h / ~ 0 years | 90.25% |
| 1h | 19h | 95.00% | 1-Feb | 400h / ~ 0 years | 99.75% |
| 1h | 999h | 99.99% | 2-Feb | ~ 500h / ~ 0 years | 99.80% |
| 1h | 19h | 95.00% | 2-Apr | ~ 2,000h / ~ 0 years | 99.95% |
| 1h | 19h | 95.00% | 2-May | ~ 33,000h / ~ 4 years | 99.99....% |
Table 1 — Comparison of probability that a system is up given systems of redundant and hardened nodes. ‘m’ nodes are required for service, ‘n’ the amount of nodes in total.
Table 1 illustrates the effects of redundancy for different systems composed of nodes that have known expected uptimes and downtimes (column 1 and 2). The left side of the table illustrates per node attributes, and the right hand side the attributes of the entire system resulting from the behaviour of each node on the left side.
Rows 1-5 illustrate a system with different setups. Row 1 is the base system, and rows 2-5 illustrate improved versions of the system, where row 2 increases the capacity per node, row 3 hardens the node, and rows 4 and 5 add redundancy instead. In this case, based on the assumptions I use here, adding two more nodes for redundancy has the same effect as increasing the expected uptime from 19h to more than 999h per node. And adding one additional redundant node in row 5 increases the MTBF (+ MTTR) to around 4 years, compared to weeks for rows 2 and 3. This illustrates the scaling of security by diversity.
Now, Table 1 is more of an illustrative example with an unreasonable MTTR, as 1h is a very low number for any real world scenario. In Table 2, I compare probabilities of services or systems function based on more realistic secure systems where individual nodes take 336h / 2 weeks to restore after node failure. The system illustrated in Table 2 involves more nodes than the system in Table 1.
| Per node | At system level | ||||
| MTTR | MTBF | Probability up | m/n | MTTR + MTBF | Probability up |
| 336h | 8,760h | 96.31% | 20/25 | 156 years | 99.98% |
| 48h | 8,760h | 99.46% | 20/25 | 1.29 * 10⁶ years | 99.99....% |
| 336h | 87,600h | 99.62% | 20/25 | 7.40 * 10⁷ years | 99.99...% |
| 336h | 8,760h | 96.31% | 10/25 | 2.15 * 10¹⁵ years | 99.99...% |
| 336h | 8,760h | 96.31% | 20/50 | 6.45 * 10²⁹ years | 99.99...% |
Table 2 — Comparison of systems providing availability through capacity scaling, hardened nodes, and increased availability of nodes. ‘m’ nodes are required for service, ‘n’ the amount of nodes in total.
Notes on Table 2: Except for the first row, none of these systems deviate from nines (9) until the 7th decimal for the system-level probability of being up. I also use 8,760h, the amount of hours in a 365-day year, rather than 8,760h-336h to keep numbers constant in the table. For the purposes of this blog post the difference is negligible as I discuss magnitudes rather than the error term of the third significant figure.
Table 2 illustrates a standard system in the first row with an expected up-time of around 156 years. Each individual node of the base system is down for around two weeks (336h) per year (8,760h), which implies an uptime of 96.31% per node. This base system requires 20 nodes out of 25 nodes to be up for the systems to function properly. This leads to an expected first system failure in 156 years and a statistical uptime of 99.98%.
The latter four rows represent three different ways of improving the availability of the system. In the second and third rows, I hardened the nodes and, instead of assuming that a node is down two weeks per year due to maintenance, repairs or similar, I altered the second row to two days (48h) per year and the third row to two weeks per ten years. Both of these modifications bring the system uptime to above 99.99% and into the millions of years (order of magnitude of 6). The fourth row illustrates a doubling of the capacity per node, so that instead of 20 nodes needed to provide the service, only 10 are needed. This increases the time between failures, the MTBF, from 156 years to more than a quadrillion years (order of magnitude of 15). As a comparison, the age of the universe is roughly 13 billion years (order of magnitude of 10). The fifth row is an example of doubling the available nodes, from 25 to 50, which increases the MTBF from 156 years to almost 10-to-the-power-of-30 years, a time period so absurd that proton decay has started and the universe is nearing a post-matter epoch.
It should be noted that the above is a statistical exercise based on known knowns and assumed independence of nodes, and in reality, all nodes of a system are not independent and there are known unknowns and unknown unknowns. For example, nodes could be using the same control or provisioning system, which could provide a point of failure with much lower redundancy.
Now, many Internet standards are designed for robustness through diversity and redundancy. That will be the topic of a future blog post in this series.
The calculations above are based on known knowns (in the tables, made up numbers for the examples, but in the real world measurable up- and down-times); it is possible to also adjust for known unknowns (by, for example, adjusting the node uptimes to a scenario where an antagonist is trying to bring down nodes, which might modify node uptime from 95% to 70% or so), but decidedly harder to mitigate the unknown unknowns. The later rows, and especially the last row, in Table 2 are examples of systems designed with an MTBF of a gazillion years for known knowns, systems which are likely to withstand even unknown unknowns.
Summary
This blog post introduces security by diversity as a concept and illustrates how nodes that individually are insecure together can provide a secure system. Through diversity, it is possible to build systems that statistically are not going to fail, ever, based on known knowns and that are likely to withstand even unknown unknowns.
Compared to hardening or increasing the capacity of individual nodes, adding additional nodes (and by that increasing the diversity) has a greater impact on expected system uptime and robustness.
The next blog post in this series will discuss the business aspects of security by diversity in a digital world, in particular, focusing on the context of the business decision on whether to use in-house or contracted resources to build secure systems.
Fredrik Lindeberg is a Security Expert in Netnod’s Security Engineering team.
This post is adapted from the original at Netnod blog.
The views expressed by the authors of this blog are their own and do not necessarily reflect the views of APNIC. Please note a Code of Conduct applies to this blog.
