The world of cryptographic algorithms constantly evolves.
In part, evolution is required by the nature of the process. The practical objective of these algorithms is not to pose a problem that is insoluble, but to pose a problem that is computationally unworkable. For example, a problem that required an enumerative search through a billion candidate answers may have been unfeasible to a computer of the 1950s but would be readily soluble with a processor used in mobile devices today.
Most forms of cryptography want to be resistant to current computational capacity, and resistant to what we anticipate being computational capacity in the coming years. How far into the future you may want to keep the cipher code a secret determines what you think is a suitably strong cryptographic algorithm setting.
Much of the encryption on the Internet these days is provided using the Rivest-Shamir-Adleman (RSA) public key crypto systems, which is also one of the oldest in this area. RSA was first described publicly in 1977 and bears the names of the mathematicians who designed it.
RSA is a public-key algorithm whose cryptographic strength is based on the practical difficulty in factoring a number that is the product of two large prime numbers. What is suitably strong encryption using the RSA algorithm has changed over the years to use increasingly large key sizes. These days, 2,048-bit keys are regarded as the minimum acceptable size for RSA keys. This implies that systems using RSA need to cope with larger keys and larger digital signatures. This increasing key and signature size can present practical issues in size-sensitive applications, such as signing DNS records in the DNS and passing these signatures over the DNS protocol.
The response to this escalation in key sizes is to look at alternative forms of public-key algorithms that have a higher cryptographic ‘density’. By this I mean that comparable cryptographic ‘strength’ can be obtained with shorter keys than the RSA equivalent, which leads us to Elliptical Curve Cryptography.
ECDSA cryptography
Elliptic Curve Digital Signature Algorithm (ECDSA) is a digital signature algorithm based on a form of cryptography termed Elliptical Curve Cryptography (ECC). This form of cryptography is based on the algebraic structure of elliptic curves over finite fields.
The security of ECC depends on the ability to compute an elliptic curve point multiplication and the practical inability to compute the multiplicand given the original and product points. This is phrased as a discrete logarithm problem, solving the equation bk = g for integer k when b and g are members of a finite group. Computing a solution for certain discrete logarithm problems is believed to be difficult, to the extent that no efficient general method for computing discrete logarithms on conventional computers is known (outside of potential approaches using quantum computing, of course). The size of the elliptic curve determines the difficulty of the problem.
The major attraction of ECDSA is not necessarily in terms of any claims of superior robustness of the algorithm as compared to RSA, but in the observation that Elliptic Curve Cryptography allows for comparably difficult problems to be represented by considerably shorter key lengths. If the length of the keys being used is a problem, then maybe ECC is a possible solution.
“Current estimates are that ECDSA with curve P-256 has an approximate equivalent strength to RSA with 3,072-bit keys. Using ECDSA with curve P-256 in DNSSEC has some advantages and disadvantages relative to using RSA with SHA-256 and with 3,072-bit keys. ECDSA keys are much shorter than RSA keys; at this size, the difference is 256 versus 3,072 bits. Similarly, ECDSA signatures are much shorter than RSA signatures. This is relevant because DNSSEC stores and transmits both keys and signatures.“
RFC 6605, Elliptic Curve Digital Signature Algorithm (DSA) for DNSSEC, P. Hoffman, W.C.A. Wijngaards, April 2012.
We are probably justified in being concerned about ever-expanding key sizes in RSA, and the associated implications of the consequent forced use of UDP fragments for the DNS, when packing those longer key values into DNSSEC-signed responses. As already noted, if UDP fragmentation in the DNS is unpalatable, then TCP for the DNS may not be much better, given that we have no clear idea of the scalability issues in replacing the stateless datagram transaction model of the DNS with that of a session state associated with each and every DNS query. The combination of these factors makes the shorter key sizes in ECDSA an attractive cryptographic algorithm for use in DNSSEC.
ECDSA has a background of patents and Intellectual Property Rights (IPR) claims, particularly — but not entirely — associated with the entity Certicom. For some time, this IPR confusion was considered sufficient reason to include ECDSA support in many distributions of crypto libraries.
OpenSSL, the most widely adopted open crypto library, added ECDSA from version 0.9.8 in 2005, but a number of software distributions took longer to decide that it was appropriate to include ECDSA support (such as Red Hat Fedora, where the distribution’s inclusion of ECDSA support was apparently delayed until late 2013, probably due to these IPR concerns).
Taking all this into account, it’s not surprising that in the past the approach to ECDSA has been cautious, both to use it as a signing algorithm and to support its use in various crypto validation libraries.
But if neither RSA nor ECDSA are to your taste, are there any viable alternatives to these two algorithms?
EdDSA algorithms
The Edwards-curve Digital Signature Algorithm (EdDSA) is a more recent offering, first published in 2011. EdDSA is a member of the elliptic-curve cryptographic family of algorithms, designed to be faster than other algorithms, unencumbered by IPR disputes and available in public domain source form.
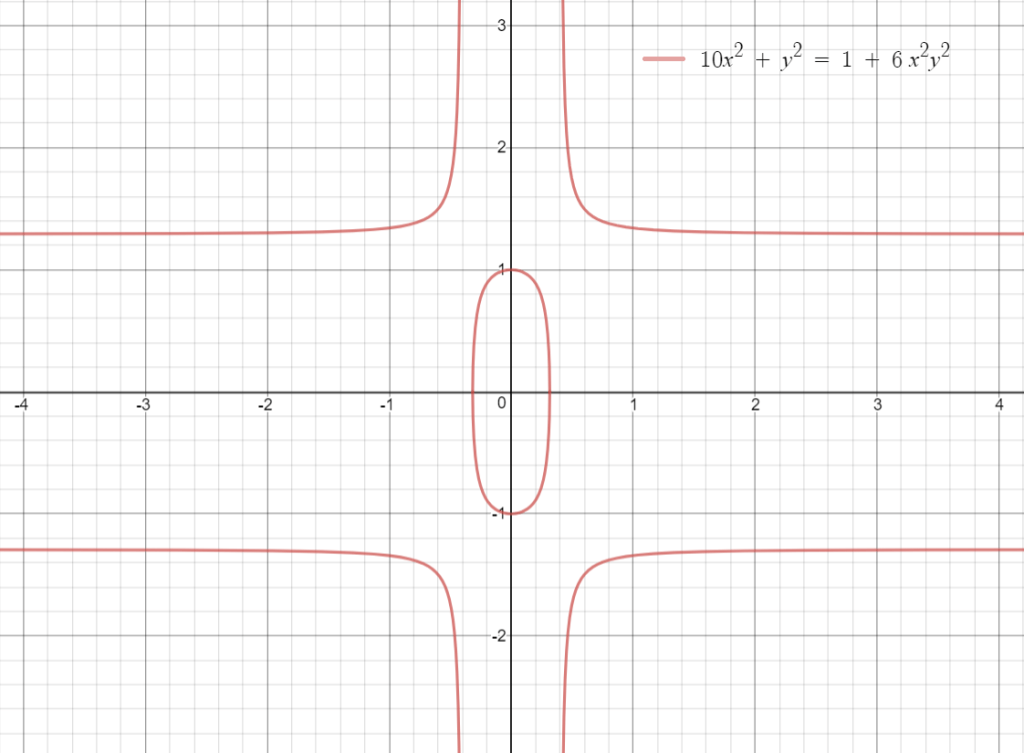
This algorithm uses a ‘Twisted Edwards Curve’.
The normal form of elliptic curves that Harold Edwards studied in 2007 was x2 + y2 = c2 + c2x2y2. The twisted transform of such curves results from the relationship ax2 + y2 = 1 + dx2y2. These curves can be used to derive a digital signature algorithm for use in public key cryptography, described in RFC 8032.
Ed25519 uses an instance of this curve where a = -1 and d = -121665/121666 and is mapped into a prime field p where p = 2255 – 19. This produces the relationship: -x2 + y2 = 1 – (121665/121666) x2y2 (mod 2255 – 19).
If EdDSA algorithms give an equivalent level of cryptographic strength to other elliptical curve algorithms and are said to be faster to compute, then should we all be using EdDSA for our crypto applications? Indeed, do we support this family of algorithms today? Or, to pose the question in a different manner — if I generated a digital signature using an EdDSA crypto algorithm, how many users on the Internet are using DNS services that can validate such a signature?
Edwards curve cryptography is a more recent algorithm than ECDSA, with the relevant standard specification for use in DNSSEC, RFC 8080, published in February 2017. Given that it takes some time for these algorithms to be accepted as robust, it might be that support for Edwards curve cryptography is not as widespread as the ECDSA or RSA algorithms. Support in OpenSSL for Ed25519 and ED448 was only released in late 2018.
On the other hand, there are only a few crypto libraries in use and there are constant reminders to keep the local copies of these libraries up to date because of the risk of exploiting known vulnerabilities in older versions. If we are all keeping such software libraries up to date, then support for Edwards curve cryptography should already be as widespread as Elliptic curve cryptography.
Which leads to the question of what is happening with deployment of tool libraries that support these recent crypto algorithms, and EdDSA in particular?
That is what I would like to investigate here, using DNSSEC as the service substrate.
EdDSA measurements
Let’s look at a comparison of ECDSA P-256 and Ed25519 in a little more detail.
Firstly, let’s look at computational performance to sign a zone file. Here, I’ll use the OpenSSL 1.1.1k libraries on a FreeBSD 12.2 host, with the DNSSEC tools supplied with Bind 9.16.16. It’s the elapsed time to perform a DNSSEC function across each of the three crypto algorithms being used that is important here, not the absolute numbers for elapsed time. Here we use NSEC signing rather than NSEC3 across a zone with 500,000 entries.
| Algorithm | Signing time | Signed zone size |
| RSA SHA256 with 2,048-bit keys | 3,200 seconds | 800Kbytes |
| ECDSA P-265 | 450 seconds | 350Kbytes |
| Ed25519 | 810 seconds | 350Kbytes |
Table 1 — Elapsed time to perform a DNSSEC function across cryptographic algorithms, using NSEC signing.
Clearly RSA gets a whole lot slower with larger key sizes. It’s also the case that Ed25519 takes roughly twice the time to sign a zone as ECDSA P-256. If you are after high(er) speed and smaller record sizes when signing a zone, then ECDSA P-256 is looking pretty good from this perspective.
What about validation performance across these algorithms?
| Algorithm | Signing time |
| Unsigned | 872 seconds |
| RSA | 878 seconds |
| ECDSA | 884 seconds |
| Ed25519 | 878 seconds |
Table 2 — Validation performance of RSA, ECDSA, and Ed25519.
Here we performed a query for 50,000 domain names in zones signed by each of the crypto algorithms using a local validating resolver. In this case it appears that the bulk of the elapsed time lies in the DNS transaction to retrieve the resource records and generate a result (872 seconds, or 17.44ms per resolved name without any form of DNSSEC validation. ECDSA validation adds a further 0.24ms per signed name, while both RSA (with 2,048-bit keys) and Ed25519 add a further 0.12ms per signed name, or one half the additional average validation time.
As well as questioning the implementation performance of these crypto algorithms we must also question the extent to which the algorithm is recognized by recursive resolvers. What proportion of the Internet’s end users are using security-aware DNS resolvers capable of handling objects signed using the EdDSA protocol, as compared to the current level of support for the ECDSA protocol?
We have switched the default DNSSEC signature algorithm in our DNSSEC validation measurement to ECDSA P-256 as of 1 December 2020, on the basis that any residual issues with ECDSA support were more than countered by the advantages of smaller DNS responses when carrying ECDSA digital signatures. We observed no discontinuity in the DNSSEC numbers from our measurement on the day we switched algorithms.
At APNIC Labs, we’ve been continuously measuring the extent of deployment of DNSSEC for more than seven years. The measurement is undertaken using an online advertising network to pass the user’s browser a very small set of tasks to perform in the background that are phrased as the retrieval of simple URLs of invisible web ‘blots’. The DNS names loaded up in each ad impression are unique, so that DNS caches do not mask out client DNS requests from the authoritative name servers, and the subsequent URL fetch (assuming that the DNS name resolution was successful) is also a uniquely named URL, so it will be served from the associated named web server and not from some intermediate web proxy.
The DNSSEC test uses three URLs:
- control URL using an unsigned DNS name
- positive URL, which uses a DNSSEC-signed DNS name (signed with ECDSA-P256)
- negative URL that uses a deliberately invalidly signed DNS name (signed with ECDSA-P256)
A user who exclusively uses DNSSEC validating resolvers will fetch the first two URLs but not the third (as the DNS name for the third cannot be successfully resolved by DNSSEC-validating resolvers, due to its corrupted digital signature).
In other DNS scenarios, a SERVFAIL response means ‘the server you have selected is unable to answer you’, which client resolvers interpret as a signal to resend the query to another server. Given that the validation failure will happen for all DNSSEC-enabled queries, the client stub resolver should iterate through all configured recursive resolvers while it attempts to resolve the name. If any of the resolvers is not performing DNSSEC validation, the client will be able to resolve the name. So, only users who exclusively use DNSSEC-validating resolvers will fail to resolve this negative DNS name.
The authoritative name servers for these DNS names will see queries for the DNSSEC RRs (in particular, DNSKEY and DS) for the latter two URLs, assuming of course that the DNS name is unique and therefore is not held in any DNS resolver cache).
To test the extent to which Ed25519 is supported we added two further tests to this set:
- A validly signed URL where the terminal zone is signed using Ed25519 (protocol number 15 in the DNSSEC algorithm protocol registry)
- A second URL where the Ed25519 signature is deliberately corrupted
What do these security-aware DNS resolvers do when they are confronted with a DNSSEC-signed zone whose signing algorithm is one they don’t recognize? RFC 4035 provides the answer to this question:
“If the resolver does not support any of the algorithms listed in an authenticated DS RRset, then the resolver will not be able to verify the authentication path to the child zone. In this case, the resolver SHOULD treat the child zone as if it were unsigned.“
RFC 4035, Protocol Modifications for the DNS Security Extensions, R. Arends, and others, March 2005.
A DNSSEC-validating DNS resolver that does not recognize the Ed25519 algorithm should still fetch the DS record of the parent zone but will then complete the resolution function as if the name were unsigned and it will return the resolution response.
We should expect to see a user who uses DNS resolvers that do not support the Ed25519 algorithm to fetch the web objects for both URLs.
An Ed25519-aware DNSSEC-validating resolver should fetch both the DS records of the parent zone and the DNSKEY record of the zone. As the resolver(s) will return SERVFAIL for the invalidly signed name, only the validly signed name will result in a web fetch of the corresponding URL (assuming all the resolvers in the resolution set accessed by this user DNS query all support Ed25519).
Ed25519 validation results
The results shown below reflect a measurement undertaken over 40 days spanning May and June 2021. The first is the daily measure of users who use resolvers that will validate DNS responses that are signed with Ed25519, compared with the daily measure of users who are validating responses using ECDSA P-256, shown in Figure 2.
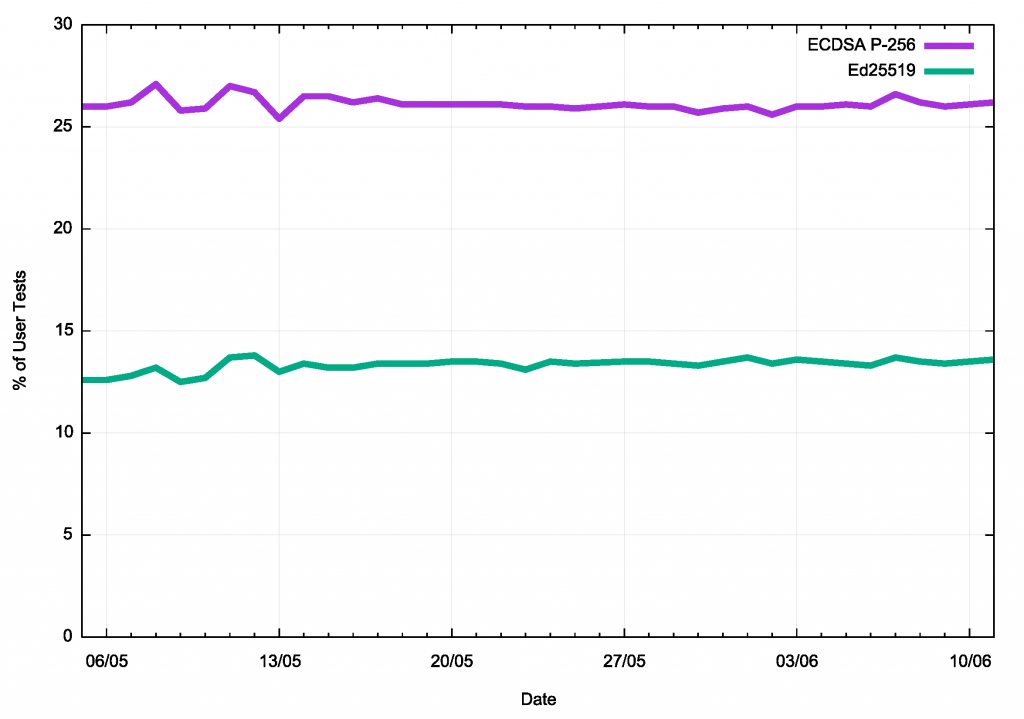
Figure 3 shows the ratio between these two measurements.
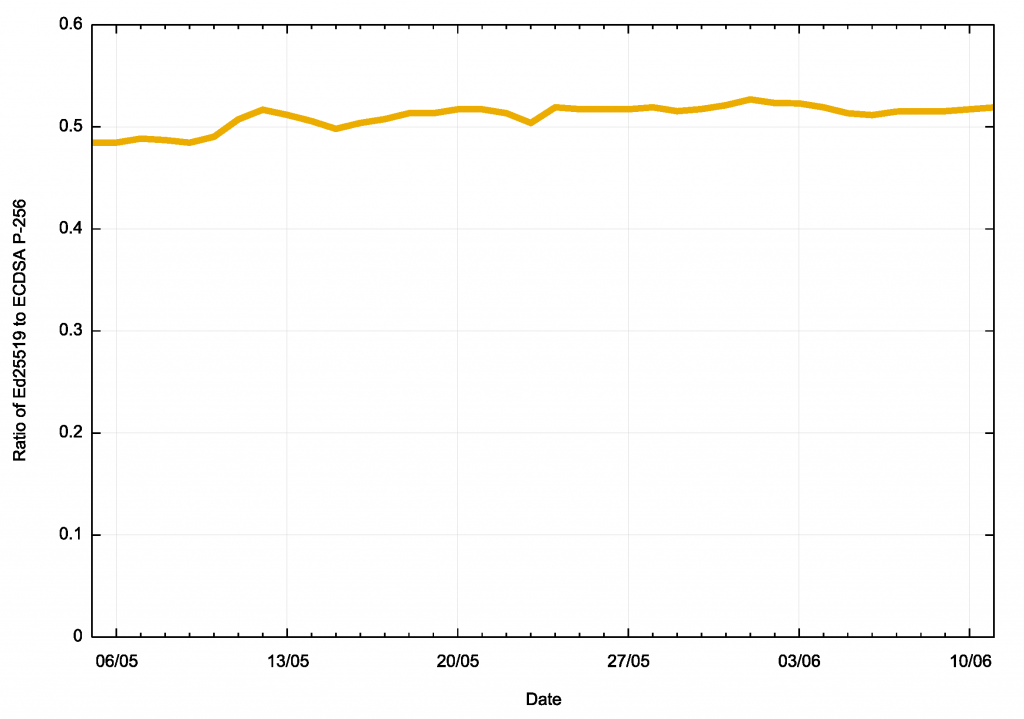
This is an unexpected result, indicating that slightly less than one half of all users who use DNS recursive resolvers that perform DNSSEC validation using ECDSA P-256 also treat Ed25519 digital signatures as ‘unknown’.
Often, Internet-wide values hide a wealth of detail and there are very few cases where a global measurement is faithfully repeated in every region and in every network. Normally, there is a high level of diversity when we take a detailed look at these various environments, and support for Ed25519 is no exception.
In Figure 4, we generated a world map with a colour scheme based on the level of support for Ed25519 in the resolvers, used by the various national user populations. The areas with high-use rates are coloured green, and low-use rates are coloured red. For high-use rate regions, it appears there is a mixture of national environments where intensive use is made of open DNS resolver services that support DNSSEC validation using Ed25519, such as Google’s 8.8.8.8 service, and environments where there is DNSSEC validation support for Ed25519 in the Intrusion Prevention System’s DNS resolver environment.
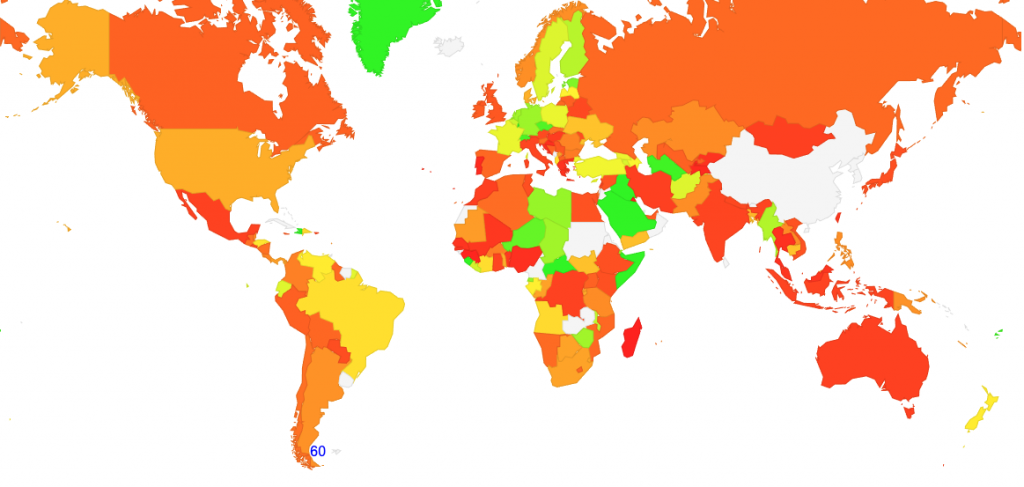
Let’s break this down and look at the economies where those using non Ed25519-aware DNS resolvers are located. The ‘ratio’ column refers to the ratio between the proportion of ECDSA-aware tests and Ed25519-aware tests. Low numbers indicate there is validation occurring but not with Ed25519 signed records, and high numbers indicate matching support for both crypto algorithms.
| CC Code | Ratio | Count | Name |
| CW | 0 | 1,052 | Curacao |
| GL | 0 | 2,238 | Greenland |
| LC | 0 | 815 | Saint Lucia |
| HT | 0 | 53,304 | Haiti |
| CF | 0 | 10,979 | Central African Republic |
| SR | 0.01 | 1,380 | Suriname |
| PF | 0.01 | 8,923 | French Polynesia |
| VI | 0.01 | 1,321 | United States Virgin Islands |
| CG | 0.01 | 6,228 | Congo |
| SL | 0.01 | 85,526 | Sierra Leone |
| AW | 0.01 | 6,176 | Aruba |
| SX | 0.01 | 1,003 | Sint Maarten |
| PE | 0.01 | 120,236 | Peru |
| GA | 0.02 | 21,263 | Gabon |
| SD | 0.02 | 34,113 | Sudan |
| CI | 0.02 | 207,957 | Cote d’Ivoire |
| TD | 0.02 | 40,283 | Chad |
| ML | 0.02 | 10,046 | Mali |
| GF | 0.02 | 3,328 | French Guiana |
| BO | 0.03 | 43381 | Bolivia |
| AO | 0.03 | 86,031 | Angola |
| LY | 0.03 | 45,452 | Libya |
| DZ | 0.03 | 191,160 | Algeria |
| PA | 0.04 | 32,860 | Panama |
| CL | 0.04 | 133,129 | Chile |
Table 3 — Economies where those using non-Ed25519-aware DNS resolvers are located.
Table 4 shows the 25 economies with the highest level of support for both crypto algorithms:
| CC Code | Ratio | Count | Name |
| WS | 0.99 | 1,733 | Samoa |
| KW | 0.97 | 79,551 | Kuwait |
| BT | 0.96 | 21,411 | Bhutan |
| BS | 0.96 | 14,872 | Bahamas |
| KN | 0.95 | 2,154 | Saint Kitts and Nevis |
| YT | 0.95 | 2,767 | Mayotte |
| IS | 0.94 | 17,896 | Iceland |
| LI | 0.93 | 1,452 | Liechtenstein |
| MN | 0.93 | 32,019 | Mongolia |
| TJ | 0.92 | 49,355 | Tajikistan |
| BJ | 0.92 | 89,362 | Benin |
| PT | 0.91 | 179,247 | Portugal |
| KI | 0.91 | 851 | Kiribati |
| BH | 0.91 | 18,526 | Bahrain |
| BB | 0.9 | 5,386 | Barbados |
| TO | 0.89 | 1,379 | Tonga |
| MA | 0.89 | 886,140 | Morocco |
| IN | 0.89 | 19,659,273 | India |
| IR | 0.86 | 632,456 | Iran |
| FO | 0.84 | 2,782 | Faeroe Islands |
| GG | 0.84 | 1,625 | Guernsey |
| MG | 0.83 | 17,317 | Madagascar |
| TL | 0.83 | 8,855 | Timor-Leste |
| MU | 0.82 | 37,108 | Mauritius |
| BF | 0.81 | 190,642 | Burkina Faso |
Table 4 — Level of support for both crypto algorithms in economies.
Let’s break down this data into ASNs. The following table lists the ASes, ranked by the number of users tested, where we observe a relatively high level of support for DNSSEC validation using ECDSA P-256 but a low level of support for Ed25519.
| AS | CC | Count | ECDSA | Ratio | Ed25519 | Ratio | AS Name |
| 55836 | IN | 22,998,060 | 21,848,577 | 0.95 | 899,647 | 0.04 | Reliance Jio, India |
| 7922 | US | 4,070,748 | 3,975,062 | 0.98 | 251,901 | 0.06 | COMCAST, USA |
| 36903 | MA | 2,070,044 | 16,77,701 | 0.81 | 148,415 | 0.07 | MT-MPLS, Morocco |
| 36992 | EG | 885,949 | 393,591 | 0.44 | 64,321 | 0.07 | ETISALAT-MISR, Egypt |
| 45245 | BD | 851,055 | 670,971 | 0.79 | 22,466 | 0.03 | BANGLALINK, Bangladesh |
| 4818 | MY | 657,060 | 610,952 | 0.93 | 9,234 | 0.01 | DIGIIX, Malaysia |
| 3243 | PT | 614,634 | 605,322 | 0.98 | 11,220 | 0.02 | MEO-RESIDENCIAL, Portugal |
| 30689 | JM | 604,787 | 370,476 | 0.61 | 48,738 | 0.08 | FLOW-NET, Jamacia |
| 45727 | ID | 599,026 | 281,679 | 0.47 | 27,017 | 0.05 | Hutchison, Indonesia |
| 35819 | SA | 524,105 | 471,071 | 0.9 | 13,819 | 0.03 | Etihad Etisalat, Saudi Arabia |
| 25144 | BA | 416,270 | 174,427 | 0.42 | 38,926 | 0.09 | TELEKOM-SRPSKE, Bosnia |
| 43766 | SA | 330,041 | 309,512 | 0.94 | 10,440 | 0.03 | MTC-KSA, Saudi Arabia |
| 8359 | RU | 281,142 | 273,762 | 0.97 | 4,561 | 0.02 | MTS, Russia |
| 23889 | MU | 272,176 | 267,050 | 0.98 | 7,127 | 0.03 | Mauritius Telecom, Mauritius |
| 17882 | MN | 255,505 | 203,365 | 0.8 | 242,29 | 0.09 | MCS, Mongolia |
| 1241 | GR | 225,024 | 221,091 | 0.98 | 6,626 | 0.03 | Forthnet, Greece |
| 26615 | BR | 194,565 | 92,371 | 0.47 | 18,433 | 0.09 | TIM, Brazil |
| 37133 | TZ | 185,453 | 182,966 | 0.99 | 1,529 | 0.01 | AIRTEL, Tanzania |
| 47589 | KW | 179,303 | 152,935 | 0.85 | 1,207 | 0.01 | KTC, Kuwait |
| 4804 | AU | 154,869 | 123,355 | 0.8 | 2,380 | 0.02 | Microplex, Australia |
| 6871 | GB | 133,194 | 112,411 | 0.84 | 3,941 | 0.03 | PLUSNET, UK |
| 9231 | HK | 114,751 | 89,091 | 0.78 | 846 | 0.01 | China Mobile Hong Kong, Hong |
| 39603 | PL | 114,310 | 112,859 | 0.99 | 1,380 | 0.01 | P4NET, Poland |
| 15146 | BS | 111,989 | 108,602 | 0.97 | 2,871 | 0.03 | CABLEBAHAMAS, Bahamas |
| 37424 | BJ | 110,672 | 107,193 | 0.97 | 933 | 0.01 | Spacetel, Benin |
| 12083 | US | 110,585 | 106,278 | 0.96 | 10,258 | 0.09 | WOW-INTERNET, USA |
| 34058 | UA | 109,748 | 108,367 | 0.99 | 1,530 | 0.01 | LIFECELL, Ukraine |
| 44143 | RS | 102,026 | 100,691 | 0.99 | 1,178 | 0.01 | A1SERBIA, Serbia |
| 16086 | FI | 99,675 | 98,390 | 0.99 | 1,233 | 0.01 | DNA, Finland |
| 29244 | BG | 97,964 | 96,725 | 0.99 | 286 | 0 | TELENORBG, Bulgaria |
Table 5 — ASes with high levels of support for DNSSEC validation using ECDSA P-256 compared to low levels of support for Ed25519.
Is Ed25519 ready for use?
What can we say about using Ed25519 as a crypto algorithm for DNSSEC?
On the positive side, the digital signatures are as small as ECDSA P-256, and DNS responses will be far smaller than comparable responses using RSA with larger keys. As a rule, smaller is better in the DNS and keeping all responses well under the packet fragmentation size is a definite positive. Ed25519, like ECDSA P-256, is a compact crypto algorithm and it certainly assists in keeping packet sizes smaller.
On the negative side, a significant proportion of users are located behind recursive resolvers that don’t recognize the Ed25519 crypto algorithm and treat the DNS response as unsigned. These same resolvers recognize ECDSA P-256, so the problem of lack of validation support is certainly one associated with Ed25519.
In my view, this data is telling us ‘No!’
If you want to take advantage of the smaller signature sizes offered by these curve-based crypto algorithms, then ECDSA P-256 appears to offer similar cryptographic strength with the same key sizes as Ed25519, but with a far more widespread support base for validation.
The relatively low integration of support levels for Ed25519 in DNSSEC-aware validating resolvers will probably change in the coming months. There are evidently ISP DNS resolution products, such as Akamai’s Cacheserve, that have recently introduced support for this particular algorithm, and it may take some time for the various ISP customers of this service to roll out the relevant upgrades across their DNS infrastructure.
However, if you are looking for a more compact DNSSEC crypto algorithm to sign your zone because you’d prefer to avoid the DNS UDP size issues associated with key rolls using RSA with 2,048-bit keys, then ECDSA P-256 would be a better choice, for a broader level of support across the DNS resolution landscape today.
The views expressed by the authors of this blog are their own and do not necessarily reflect the views of APNIC. Please note a Code of Conduct applies to this blog.
