
Internet routing has its mysteries. One of them is that commonly used routing protocols such as Border Gateway Protocol (BGP), Enhanced Interior Gateway Routing Protocol (EIGRP), and Open Shortest Path First (OSPF), fail to find optimal paths across a network.
Less than optimal routing protocols
This is not the case with standard additive metrics, such as delay or hop-count, but consider the following example (Figure 1) involving an additive and a bottleneck metric, such as available bandwidth or capacity.
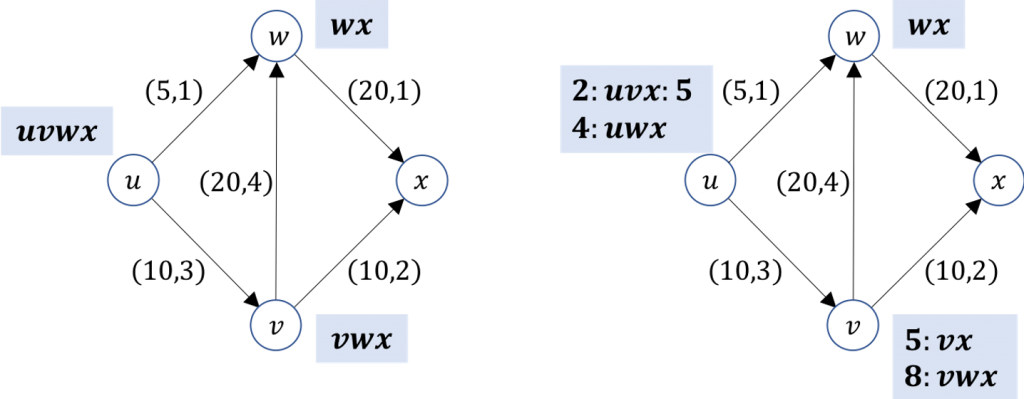
Every link in the example is annotated with a pair width-length. The width of a path is the minimum of the widths of its links and the length of path is the sum of the lengths of its links. There are three paths from u to x:
- path uvx, with width-length (min(10,10), 3 + 2) = (10, 5)
- path uwx, with width-length (min(5, 20), 1 + 1) = (5, 2)
- path uvwx, with width-length (min(10, 20, 20), 3 + 4 + 1) = (10, 8)
Suppose an optimality criterion that derives from a preference for widest paths and, in case of a tie between widths, for a preference for the shortest of widest paths. The shortest of widest paths from u to x is uvx .
In a standard vectoring protocol (left-hand side of the figure), such as BGP or EIGRP, node v learns path vx directly from x and path vwx from w. It selects path vwx because of its greater width; path vwx is advertised to u, while path vx is hidden from u. Hence, node u learns uvwx from v and selects this path, because the alternative path, which is uwx learned from w, has a smaller width. Node u forwards data-packets to v, which forwards them to w, which delivers them to x. Data-packets traverse path uvwx, which is not the shortest of widest paths from u to x.
Why did the standard vectoring protocol fail to find optimal paths?
The heart of the problem is that the preference between two paths may be flipped in their extensions to a neighbor node. In Figure 1, path vwx is preferred to path vx. However, path uvwx, which is the extension of vwx to node u, is not preferred to path uvx, which is the extension of vx to node u.
‘Isotonicity’ is the name given to the property that precludes the flipping described above, rather affirming that the preference between any two paths is preserved in their extensions to a neighbor node. A standard vectoring protocol routes optimally if, and only if, the optimality criterion satisfies isotonicity.
New optimal routing protocols
Alas, many optimality criteria of practical interest do not satisfy isotonicity. But that doesn’t stop us from trying as we at the Institute of Telecommunications, University of Lisbon, sought to design new vectoring protocols that find optimal paths in such cases.
Our idea is to abstain from the selection between any two paths whenever such a selection would violate isotonicity, trading singleness of path selection at nodes for isotonicity. In the example of the shortest of widest paths, nodes refrain from selecting between two paths if, and only if, one of them has greater width and the other has smaller length. That is the case of paths vwx and vx in Figure 1: the former has greater width and the latter has smaller length.
Using the new protocols (right-hand side of the figure), the node v advertises both vwx and vx to u. Hence, node u learns all of paths uvx, uvwx, and uwx from itself to x. It discards path uvwx, because it has the same width and greater length than those of path uvx; it retains both uvx and uwx, since the former path has greater width and the latter has smaller length. Node u chooses path uvx as the shortest of widest paths between uwx and uvx with the assurance that uvx is indeed the network-wide shortest of widest paths from u to v. Labels are advertised alongside paths to guide data-packets through label-switching.
The same idea of withholding path selections at nodes allows concurrent routing on multiple optimality criteria under a common routing protocol. The selection between two paths is abstained from whenever the various optimality criteria do not agree on which path is preferred.
Returning to the example above, suppose we add an optimality criterion that derives from a preference for shortest paths. As discussed above, node u computes paths uvx and uwx with the new protocols. For shortest paths, node u chooses path uwx with the assurance that this path is the network-wide shortest path from u to x.
Although we illustrated the new protocols with an example, our results apply to arbitrary optimality criteria and networks. We believe that this breakthrough in optimal path routing coupled with progress on network programmability provide a richer set of routing options for future networks.
To learn more please refer to our paper and video presentation ‘Routing on Multiple Optimality Criteria’, which we presented at ACM SIGCOMM 2020.
João L. Sobrinho is a Professor of the Faculty of Engineering at the University of Lisbon.
The views expressed by the authors of this blog are their own and do not necessarily reflect the views of APNIC. Please note a Code of Conduct applies to this blog.
