
It may be useful to start this article by defining what I am talking about. No, ‘Post-Quantum Cryptography’ is not about using the next generation of computer processors that may come after quantum computing, whatever that may be, to perform cryptography. It’s not even about ‘Quantum Cryptography’, which is all about devising cryptographic algorithms based on quantum mechanics. Post-Quantum Cryptography is conventional cryptography using algorithms, key sizes, and applications running on today’s processors to generate cryptographic protection over data that is resistant to the use of quantum computers to attempt to break the cryptographic code.
You might think that we should worry about this only when we’ve managed to construct quantum computers that can perform slightly more significant tasks than to find the prime factors of 21. In the world of cryptography, the major consideration is how long you want to hold a secret. If you want to encrypt a block of data and hold it as a secret for, say 20 years, then it’s not the capabilities of today’s computers you need to concern yourself with. It’s the collection of computers that we might have access to in the period from today to just under 20 years from now that is the concern.
If you used Moore’s Law as your benchmark, computing power doubling every 18 months would make computers nearly 10,000 times more capable than today’s in 20 years.
In cryptography, the aim is not to generate impossible-to-solve problems, but instead to generate problems that are easy to generate, but computationally infeasible using today’s computers. For example, it is readily possible to take two extremely large prime integers and multiply them together to make an even larger composite number, yet it is extremely challenging to reverse this and take a very large composite number and produce its prime number factors. Enumeration-style algorithms require massive amounts of time to perform such a calculation.
Now if computers are becoming twice as capable every 18 months and we want to use a cryptographic algorithm that will remain robust for 20 years, we need to look at a class of problems that are at least some 10,000 times ‘harder’ to compute than today’s class of solvable problems. This would be extraordinarily challenging if we had to devise a new cryptographic algorithm every time we wanted to generate a ‘harder’ problem, but these days we use a constant algorithm and ever larger key sizes to increase the computational complexity of attempting to break the encryption. For example, if the challenge is to generate the prime factors of a number that is 30 digits long, then the potential search space of a number that is 31 digits long is some 10 times larger. To date, we’ve responded to the challenges of Moore’s Law by a constant upgrading of the minimum key sizes used with cryptographic algorithms.
We can jump out of these increasing public key and digital signature sizes by shifting to a different cryptographic algorithm that uses a smaller key size and a smaller digital signature, but the development cost of devising a new algorithm and proving that it’s adequately robust is far harder that the process of increasing key sizes, so our algorithm choices tend to be very sticky.
This is indeed what we’ve done for the past few decades. The Rivest–Shamir–Adleman cryptosystem (RSA) is one of the oldest widely used asymmetric cryptographic algorithms used for securing data. Cryptographic algorithms have the property that it is relatively easy to encode cyphertext if you have knowledge of one of the keys, but extremely challenging to decode this cyphertext unless you already have knowledge of the complementary key.
RSA is based on integer transforms using large prime numbers, and its strength is based on the fact that finding the prime factors of a large composite number still relies on brute force enumeration. Subsequent work in cryptography has produced a digital signature algorithm that is based on Elliptical Curve Cryptography (ECC). This form of cryptography is based on the algebraic structure of elliptic curves over finite fields. The major attraction of ECC is not necessarily in terms of any claims of superior robustness of the algorithm as compared to RSA, but in the observation that ECC allows for comparably difficult problems to be represented by considerably shorter key lengths and digital signatures. If the length of the keys being used is a problem, then maybe ECC is a possible solution.
Today’s cryptographic algorithms are a tradeoff between cryptographic strength and usability. To help understand the relative strength of cryptographic algorithms and keys there is the concept of a Security Level, which is the log2 of the number of operations to solve a cryptographic challenge. In other words, a security level of n implies that it will take 2n operations to solve the cryptographic challenge. A comparison of RSA with various key sizes and a couple of ECC algorithms is shown in Table 1.
| Algorithm | Private key | Public key | Signature | Security level |
| RSA-1024 | 1,102 | 438 | 259 | 80 |
| RSA-2048 | 1,776 | 620 | 403 | 112 |
| RSA-4096 | 3,312 | 967 | 744 | 140 |
| ECDSA P-256 | 187 | 353 | 146 | 128 |
| Ed25519 | 179 | 300 | 146 | 128 |
Quantum computers
All this is fine if you assume ‘scalar’ computation, where to double the number of operations per second you either need to double the number of processors or double the processor’s clock speed. In recent times there has been considerable interest in the development of so-called quantum computers. These systems exploit quantum mechanical phenomena where a unit of information is not a classical bit with a value of 1 or 0, but a qubit that is the superposition of its two basic states simultaneously. There are many sources of descriptions of quantum computers, so I’ll not go into any further detail here, but suffice it to say that while there is much optimism that quantum computers will be refined in the coming years to the point where they can solve significant computational challenges, the current state of quantum computers is very early in its infancy! They represent the equivalent of massively parallel processing, sometimes described as parallel processing at an exponential scale.
The engineering challenges with quantum computers are significant, and progress in engineering a quantum computer has so far been slow and extremely expensive. What’s kept many projects going is the prospect that a significantly large quantum computer could solve a range of computational challenges that are simply beyond the practical reach of binary computers.
Well in advance of the engineering challenge of constructing quantum computers, academic research into the properties of quantum computers highlighted the observation that quantum computing could be significantly faster in solving certain classes of problems than classical computers. In 1994 Peter Shor published an algorithm for finding the prime factors of an integer. This algorithm has compelling potential application in cryptography when the exponential speedup compared to best-known classical (non-quantum) algorithms heralds a new era of cryptography. The implication is that cyphertext that is encrypted using RSA and ECC algorithms is susceptible to being broken once quantum computers achieve the necessary scale and reliability goals.
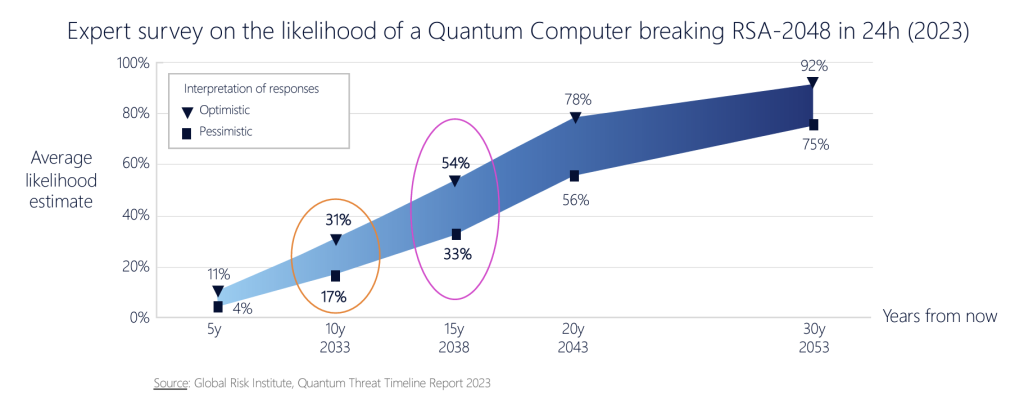
This computer is termed a Cryptographically Relevant Quantum Computer (CRQC). When that may happen is literally anyone’s guess, but the more money that gets pumped into finding solutions to the engineering issues of quantum computers, the earlier that date will be. The year 2030 has been talked about, and it is not considered to be a completely crazy date, even though it’s well on the optimistic side (Figure 1). This date is well within a two-decade horizon of keeping a secret, so if you want to ensure that what you are encrypting today remains a secret for the next twenty years, then it is prudent to assume that quantum computers will be used to try and break this secret sometime within those twenty years.
So, even though capable quantum computers are yet to be built, we need to consider the use of quantum-resistant cryptographic algorithms today in certain areas where the long-held integrity of the encryption process is important. The present danger lies in an attacker performing data capture now, in anticipation of being able to post-process it at a later date with a CRQC. There is even an acronym for this, Harvest Now, Decrypt Later (HNDL).
The development of Post-Quantum Cryptographic algorithms
The US National Institute of Standards and Technology (NIST) started its Post-Quantum Cryptography project in 2016, asking for submissions of algorithms that would prove resistant to both classical and quantum computers. By the deadline, about a year later, experts from dozens of economies had submitted 69 candidate algorithms that met NIST’s thresholds. These algorithms were then released for multiple rounds of evaluation, intended to reduce the size of this algorithm pool. It’s not just an exercise in designing an algorithm that produces cyphertext that is highly resistant to efforts to crack it, but the act of production of this cyphertext can be ported to many profiles of processors, including limited computational environments such as is found in the appliance environment of the Internet of Things, or smart cards.
In 2022, the NIST process had whittled this initial set down to four algorithms as candidates for standardization, one for key exchange and three for digital signatures. One signature algorithm was dropped by the time the final standards were published in 2024 as it was found to be breakable. We can’t be sure that the remaining three algorithms (ML-DSA, SLH-DSA and ML-KEM) are safe to use, but so far, they have not been broken!
What approach should we use for cryptography today? We can’t place long-term trust in the classical cryptographic algorithms, as they are susceptible to being broken by quantum computers at some point in the future, but at the same time, we can’t really trust the new post-quantum algorithms as yet, because they really haven’t been exposed to extensive analysis in depth. One pragmatic approach is to use a so-called hybrid approach, combining the outputs of both a classical algorithm and a post-quantum algorithm to generate the cyphertext. Even if the post-quantum algorithm is broken in the near future, the classical algorithm will still maintain its cryptographic strength until quantum computers are realized.
The second challenge is related to the parameters of these new post-quantum algorithms. They all use large key sizes and generate large signatures. ML-DSA has a key size of 1,312 bytes and a signature size of 2,430 bytes. This has a security level of 128, roughly equivalent to RSA-3072, which has a key size of 387 bytes and a signature size of 384 bytes. This can be an issue on memory-constrained devices and is certainly an issue when considering the use of UDP-based transports in applications such as DNSSEC, where the larger key size pushed the UDP transport into IP packet fragmentation with all the attendant reliability issues that are associated with fragmentation and reassembly.
Module-Lattice-Based Key-Encapsulation Mechanism (ML-KEM)
A Key-Encapsulation Mechanism (KEM) is a set of algorithms that enables two parties to establish a shared secret key over a public channel. This key can be used for secure communication tasks like encryption and authentication. ML-KEM, which relies on the Module Learning with Errors problem for its security, is believed to be secure even against quantum computers.
In the FIPS-203 standard, there are three ML-KEM parameter sets, ML-KEM-512, ML-KEM-768, and ML-KEM-1024, increasing in security but decreasing in performance. These have key and ciphertext sizes shown in Table 2.
| Parameter | Encapsulation key size | Decapsulation key size | Ciphertext size | Shared key size |
| ML-KEM-512 | 800 | 1,632 | 768 | 32 |
| ML-KEM-768 | 1,184 | 2,400 | 1,088 | 32 |
| ML-KEM-1024 | 1,568 | 3,168 | 1,568 | 32 |
Module-Lattice-Based Digital Signature Standard (ML-DSA)
Digital signatures allow us to verify data integrity and authenticate the signer’s identity. They also provide non-repudiation, meaning the signer cannot later deny the signature and the document cannot be tampered with. ML-DSA is a set of algorithms for generating and verifying digital signatures, which is believed to be secure even against quantum computer threats.
The standard FIPS-204 includes parameter sets for ML-DSA-44, ML-DSA-65 and ML-DSA-87 with key sizes shown in Table 3.
| Parameter | Private key size | Public key size | Signature size |
| ML-DSA-44 | 2,560 | 1,312 | 2,420 |
| ML-DSA-65 | 4,032 | 1,952 | 3,309 |
| ML-DSA-87 | 4,896 | 2,592 | 4,627 |
Stateless hash-based signature standard (SLH-DSA)
SLH-DSA is a hash-based digital signature algorithm that is believed to be secure against quantum computing attacks. The FIPS-205 standard describes 12 parameter sets for use with SLH-DSA, 6 using SHA2 and 6 using SHAKE.
FIPS-205 lists the key and signature sizes for SLH-DSA shown in Table 4.
| Parameter | Security category | Public key size (bytes) | Signature size (bytes) |
| SLH-DSA-SHA2-128s SLH-DSA-SHAKE-128s | 1 | 32 | 7,856 |
| SLH-DSA-SHA2-128f SLH-DSA-SHAKE-128f | 1 | 32 | 17,088 |
| SLH-DSA-SHA2-192s SLH-DSA-SHAKE-192s | 3 | 48 | 16,224 |
| SLH-DSA-SHA2-192f SLH-DSA-SHAKE-192f | 3 | 48 | 35,664 |
| SLH-DSA-SHA2-256s SLH-DSA-SHAKE-256s | 5 | 64 | 29,792 |
| SLH-DSA-SHA2-256f SLH-DSA-SHAKE-256f | 5 | 64 | 49,856 |
Application and threat models
There are two common applications of cryptography, and they have different associated threat models.
For Digital Signature Algorithms (DSA) the threat is that an attacker can construct the private key value matching the target’s public key. If the attacker is also able to intercept traffic to the target site it can successfully respond to identify challenges that have been made using the target’s public key with its own private key value and successfully impersonate the target.
If the issuing CA performs certificate renewal based on the test of proof of possession of the old private key to accept the new key pair, then the attacker can perform a certificate re-issuance and thereby isolate the original key holder from the protected asset.
If the CA’s key pair is compromised, the entire PKI framework can be at risk. In extreme cases, the only remedy may be a zero-based reset, involving the establishment of new trusted roots (CAs), re-issuance of the entire PKI set, and potentially the implementation of a new certificate management infrastructure. Obviously, such a compromise is little short of catastrophic to the entire PKI frameworks that we rely on for trust on the Internet. As long as PKI certificate lifetimes are short, the window of opportunity for such an attack is limited to the certificate lifetime period.
In theory, certificate revocation could help mitigate the impact, but in practice, consulting certificate revocation lists are uncommon in PKIs on the Internet today. This situation essentially represents a ‘real-time’ attack. If capable quantum computers become available in, say, six years, applying a bundle of current (2024) public key certificates to such a quantum computer would reveal that only certificates with extended validity periods are susceptible to a quantum attack in 2030. Short certificate lifetimes are, therefore, a valuable feature of any public PKI framework.
If we are looking at drivers for the immediate deployment of post-quantum cryptography, the digital signature application space is generally not a compelling motivation. The most practical current response to the quantum threat is to use public key certificates with reasonably short lifetimes so that the window of vulnerability to future attacks is limited.
For session key establishment the problem is somewhat different. If the entirety of a session can be captured by a third party, then the initial setup that establishes the session key is also captured. This initial setup is protected by a crypto exchange so that the generation of the session key is a private act between the two parties. The session capture can be replayed to a capable quantum computer, this would allow the session key generation to be exposed, and the entire session contents can be decoded at that time. The only defence against this attack in the future is to shift to using the quantum-resistant algorithm now, namely ML-KEM, and perform key exchange using this algorithm.
This process is already underway with today’s dominant browser platform, Google Chrome, switching from KYBER to ML-KEM for key exchange in November 2024 with version 131. The upside of this is that the changes are entirely software-based, and do not require any changes to PKI infrastructure.
Practical implications
The transition to post-quantum algorithms also presents practical challenges for software. For example, the size of key chains used to pass certificates increases significantly, from around 4 KB with RSA to 22 KB with ML-DSA. This poses a challenge for DTLS (TLS over UDP) and necessitates adjustments to QUIC. Similarly, conventional TLS over TCP would benefit from accommodating the entire initial certificate offer within the initial TCP window. Achieving this would require an initial window size of approximately 20 Maximum Segment Size (MSS) -sized packets, a significant increase from the current, more conservative value of 4 packets.
Obviously, DNSSEC presents some challenges. The large increase in the size of digital signatures implies that DNSSEC using quantum-resistant algorithms over a UDP transport is not really an operationally robust choice. This would imply that DNSSEC transactions should really be supported using TCP. Using the ‘fallback’ mechanism by first using a query over UDP and receiving a truncated response adds one round-trip delay to each DNSSEC-signed DNS transaction, and a further delay to establish the TCP session.
Perhaps it would make more sense to combine the use of the DNSSEC-OK flag in queries with the initial use of TCP in queries, bypassing UDP altogether for such queries, but there are more considerations here. In the case of the stub-to-recursive resolver the use of a long-lived TCP session allows the application to amortize the cost of the initial TCP handshake (and more if using DOH, DOQ, or DOT) across multiple subsequent queries. In the case of recursive-to-authoritative queries, the prospect of session reuse is not so great, so the overhead of session start is greater. It should also be noted that the number of stub resolvers performing DNSSEC validation is incredibly small, so the predominant use of DNSSEC is in the recursive-to-authoritative environment.
Some work has explored the novel use of Merkle Trees to reduce the size of certain DNSSEC responses. However, I find myself somewhat perplexed by the broader rationale for advocating urgency in developing post-quantum cryptographic algorithms for DNSSEC at this stage.
DNSSEC does not appear to be susceptible to the risks of HNDL in that the encrypted information provides some level of authentication of DNS data rather than providing long-term secrecy of DNS queries and responses. Breaking a DNS key allows an attacker to pass off synthetic DNS responses as authentic, but this is a real-time attack and is dependent on the timing of the deployment of CRQCs (that’s Cryptographically Relevant Quantum Computers). I suspect that for DNSSEC we are still at a time when we can work on this problem without needing to deploy a Post-Quantum Cryptography solution for DNSSEC in the short term.
I also suspect that the data in Figure 1 about the common expectations about the timing of CRQCs is missing the critical issue of the economics of quantum processing. There seems to be an expectation that quantum computing will follow similar principles to conventional computing with silicon-based integrated circuits — namely, that the unit cost of processing will decrease as clock speeds, gate densities, and track widths on chips improve. But what if quantum computers do not follow this path?
At some point, the cost of mounting an attack must be less than the value of the resources that are at risk from such an attack. If we cannot find ways to leverage scale and speed in quantum computer design, then we will be left in the position of knowing how to build such super-scaled systems based on large arrays of qubits but lacking sufficiently valuable reasons as to why to make the investment to build and operate such computers.
There is currently significant academic research activity in quantum computing and the application of Post-Quantum Cryptography. However, I suspect that the primary motivation for this level of research activity is that the successful path through various research funding bodies these days is to make liberal use of the vocabulary of quantum computing and digital security in the research funding application!
It is far less obvious to me that in most cases, and here I explicitly include DNSSEC in this, there is a reasonable justification for such research at present that is made on a more clinical evaluation of future needs. In the area of digital encryption, there is some justification for the use of Post-Quantum Cryptography with the expectation that the data being encrypted has ongoing value as a secret for the next couple of decades or more.
It is far less obvious to me — I explicitly include DNSSEC in this — that there is a reasonable justification for such research based on a more clinical evaluation of future needs. There is some justification for Post-Quantum Cryptography in digital encryption in the expectation that encrypted data will retain its value as a secret for several decades or more.
However, when the objective differs — such as timely authentication of a remote party or opportunistic encryption — it becomes much harder to justify focusing on this aspect of cryptography for DNSSEC at present. Even if a CRQC is developed in the future, if its cost to use it is eye-wateringly large, it will likely be used only in high-end, esoteric areas. In such a scenario, our future selves may regard today’s enthusiasm for shifting their attention to the real-time generation of synthetic DNS answers as misplaced.
Presentations
The presentations in recent meetings on this topic include:
NANOG 92, October 2024:
- ‘In-flight data protection in the quantum age‘, Chris Janson, Nokia (recording)
- ‘Demystifying the Quantum Threat for Network Operators‘, Rakesh Reddy Kandula, Cisco Systems (recording)
RIPE 89, October 2024:
- ‘Post-Quantum Transition: Standards, Effects on Protocols‘, Dmitry Belyavskiy, Red Hat (recording)
- ‘Field Experiments on Post-Quantum DNSSEC‘, Jason Goertzen, Peter Thomassen, Nils Wisiol, Sandbox AQ, deSEC (recording)
The views expressed by the authors of this blog are their own and do not necessarily reflect the views of APNIC. Please note a Code of Conduct applies to this blog.

Readers with an interest in the topic of Post-Quantum Cryptography and the DNS should also read the report prepared by Paul Hoffman of the ICANN Office of the CTO , published in April of 2024.
Geoff
great article