
Textbooks tell us that cache requests result in one of two possible outcomes: cache hits and misses. However, when the cache miss latency is higher than the inter-arrival time between requests, it produces a third possibility, delayed hits.
Existing literature on caching, although vast, ignores the contribution of delayed hits. In a research paper presented at SIGCOMM ‘20, we at Carnegie Mellon University in collaboration with Microsoft Research, show that this is problematic because:
- Traditional caching models underestimate the true latency cost of serving cache requests.
- They tempt cache operators to make incorrect decisions about the ‘right’ caching algorithm to deploy.
- Delayed hits subvert expectations of traditional caching algorithms, resulting in high request latencies.
Our research showed that in the presence of delayed hits, the seemingly related goals of hit rate (HR) maximization and latency-minimization are not equivalent. Thus, HR should not be the optimization criteria when designing a latency-minimizing cache.
Further, by explicitly accounting for delayed hits, we can reduce caching latencies by up to 60% compared to existing caching algorithms. We devise a novel online caching strategy, Minimum-Aggregate Delay (MAD), which realizes these latency improvements.
Key points:
- In high-performance caches (where delayed hits are prevalent), maximizing hit rate does not necessarily minimize average latency.
- Delayed hits-aware algorithms — such as MAD — can provide significant latency improvements over existing caching algorithms.
What are delayed hits?
Delayed hits occur when multiple requests to the same object arrive before an outstanding cache miss is resolved.
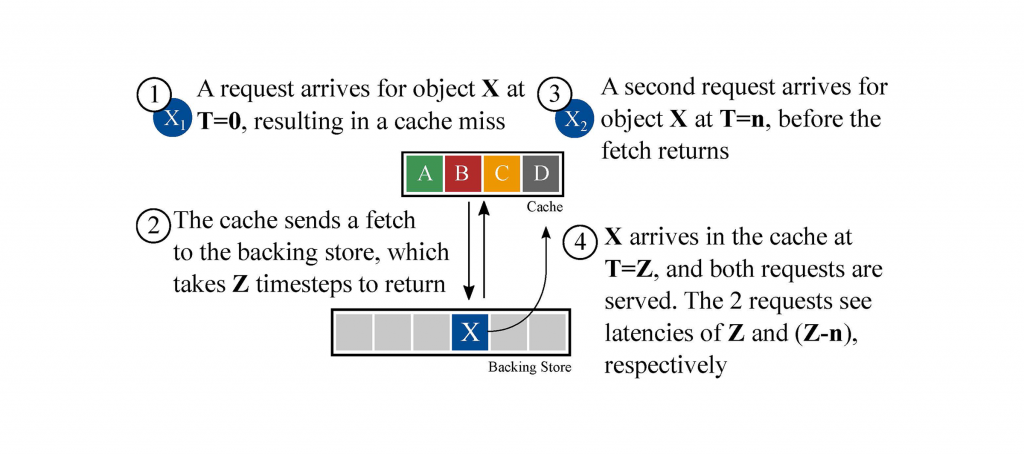
Figure 1 — A basic delayed hit scenario. When a request arrives for an object that is not cached ①, it triggers a fetch to retrieve this object from a backing store ②. The retrieval takes some non-zero amount of time, L seconds, and the average inter-arrival time between requests (IRT) is R seconds. For simplicity, we say that R seconds is one ‘timestep’, and that the amount of time required to fetch the object is Z = L/R timesteps. After the object is requested, but before Z timesteps have completed, a new request arrives ③. This request must wait for some non-zero, but <Z amount of time for the object to arrive in the cache ④. According to traditional caching literature, the second request for object X (at time T=n) would be counted as a cache hit; in reality, this request experiences a slower, delayed hit with non-zero latency.
In Figure 1, Z represents the maximum number of outstanding cache requests (and therefore, delayed hits) that can occur while a fetch is in progress. Table 1 lists a few examples of Z values one might see in practice.
| Scenario | Use Case | Latency | Z |
|---|---|---|---|
| CDN (IRT = 1 μs) |
Intra-data centre proxy | 1 ms | 1K |
| Forward proxy to a remote data centre | 200 ms | 200K | |
| Network (IRT = 3 μs) |
Single DRAM lookup | 100 ns | <1 |
| IDS with reverse DNS lookup | 200 ns | 67K | |
| Storage (IRT = 30 μs) |
Cross-data centre file system access | 150 ms | 5K |
Table 1 — Examples of a maximum number of outstanding cache requests (Z) that can occur while a fetch is in progress.
Empirically, we see that as Z increases, so does the number (and impact) of delayed hits. It is important to note that Z can go up either due to an increase in backing store latency, a decrease in request inter-arrival time (higher bandwidth), or both.
Delayed hits, hit rate, and average latency
Delayed hits subvert expectations of traditional caching models when it comes to latency.
Recall that the cache HR is defined as the ratio of the number of cache hits to the total number of requests served by the cache. Traditional caching models tell us that we can compute average request latency using the Average Memory Access Time (AMAT) expression. Unfortunately, in the presence of delayed hits, this expression is no longer accurate; we find that latency estimates derived from HR-based models underestimate true latency.
Figure 2 depicts two simulated models using the Least-Recently Used (LRU) caching algorithm — one that accounts for delayed hits, labelled ‘Actual’, and one that does not, labelled ‘Idealized’.
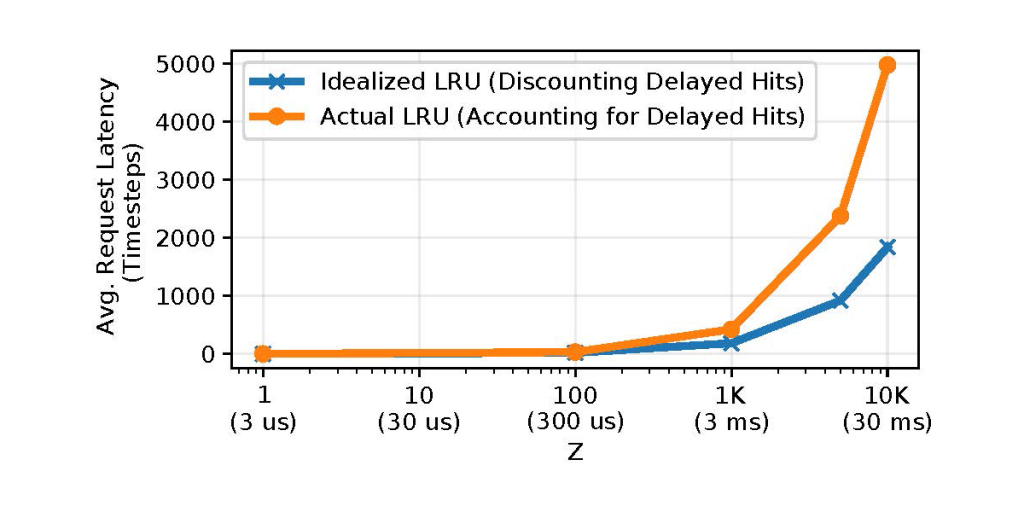
On the y-axis, we plot the average request latency, and on the x-axis, we sweep Z. As Z increases, the latency estimates derived from HR (‘Idealized’) quickly diverge from their actual values; at Z=10K, the error exceeds 60%. Consequently, relying on HR to estimate average request latency can introduce significant error, not just in simulations, but also in real systems.
Moreover, we find that traditional caching models may mislead cache operators when it comes to choosing the ‘right’ algorithm to deploy.
For instance, Alice wants to decide between two algorithms, α and β, for her latency-minimizing cache. Empirically, she observes that α achieves a better (higher) hit rate than β for her workload. Based on the expression for average latency, she concludes that α must also achieve better (lower) latency. Is her conclusion correct?
Perhaps surprisingly, it might not be! In the presence of delayed hits, α might, in fact, perform worse in terms of latency. This is because when delayed hits occur, optimizing for hit rate is a fundamentally different problem than optimizing for latency.
Can we do better?
Existing caching algorithms, like their underlying models, do not account for delayed hits, and, as a result, they are prone to making latency-suboptimal decisions. Then, a natural question is: can we outperform existing caching algorithms by explicitly accounting for delayed hits?
Through analysis of the offline delayed hits problem, we found from our study that delayed hits-aware algorithms can provide substantially lower latencies than the algorithms deployed today. In the offline setting, we observed improvements of up to 45%.
This analysis also enabled us to design an online caching strategy, MAD, that makes existing algorithms aware of delayed hits, yielding significant improvements (10 — 60% lower latencies) in the process. The following figures depict the latency improvements provided by MAD variants of three popular caching algorithms (LRU, Adaptive Replacement Cache (ARC), and Least Hit Density (LHD)) for two application scenarios: a 10Gbps Network, and a Content Delivery Network (CDN).
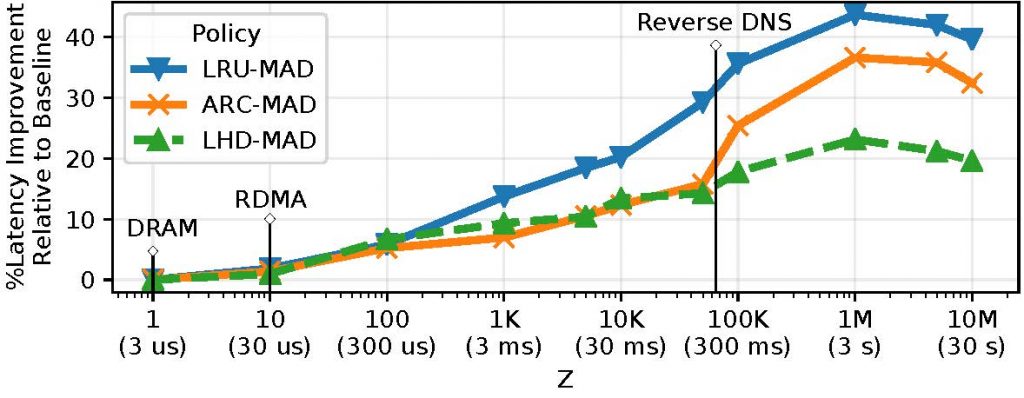
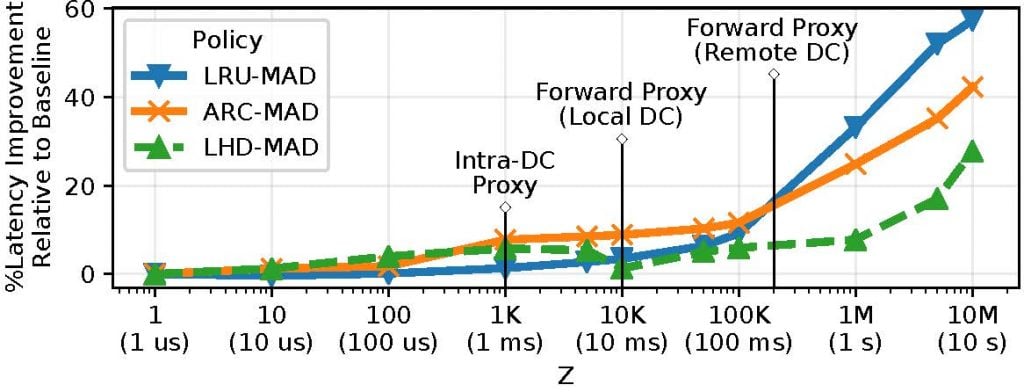
Is there a tradeoff?
We saw that MAD consistently outperforms existing caching algorithms in terms of latency. However, as is typical in the systems design space, this improvement does not (always) come for free.
Since optimizing for HR and latency are fundamentally different problems, MAD may inflate the miss rate, which in turn is proportional to the bandwidth usage on the link to the backing store. Figure 4 depicts the relative increase in miss rate due to MAD in the 10Gbps network scenario (regions highlighted red indicate higher miss rates).
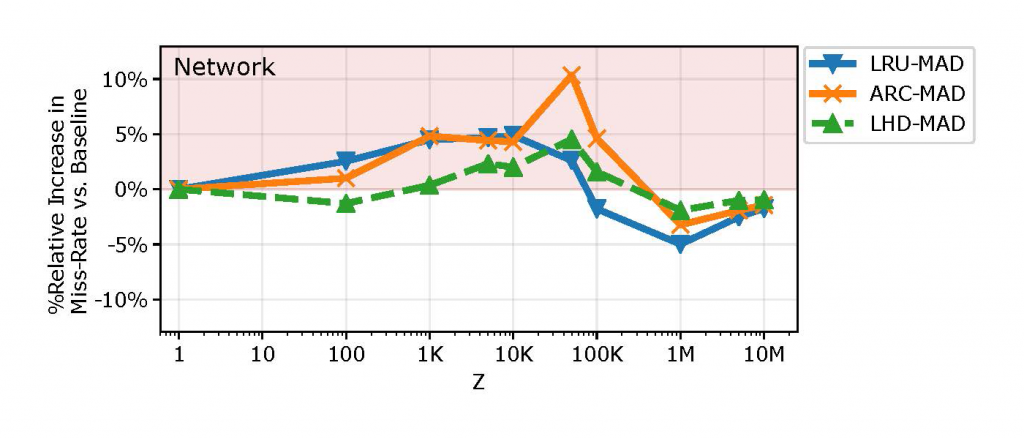
Here, MAD inflates the miss rate by up to 10% relative to the baseline miss rate (+1.84% on average).
However, this is not always the case. Figure 5 depicts MAD’s behaviour in the CDN setting.
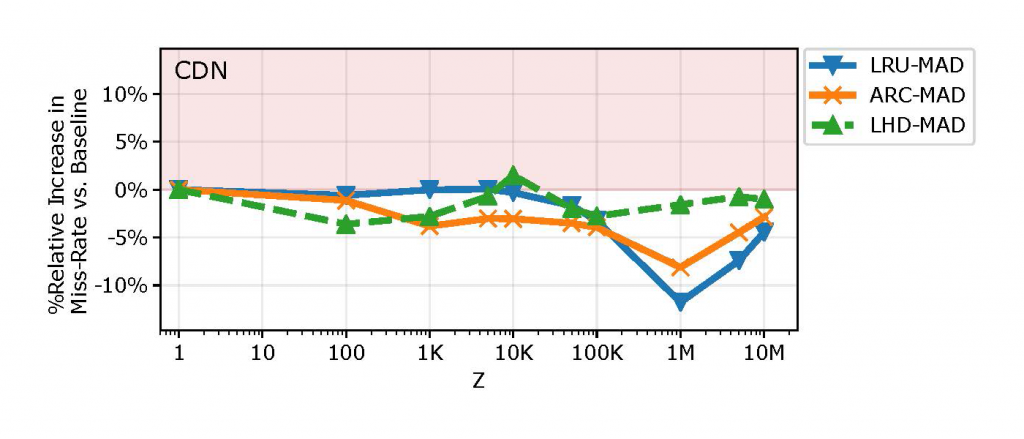
Here, not only does MAD provide significantly lower latencies, but almost always reduces miss rates (by up to 10%). We conclude that there might be a latency-bandwidth tradeoff depending on the scenario, baseline algorithm, and operational Z value.
If you would like to experiment with MAD, you can find our implementation of it (in simulation) on our GitHub.
To learn more about this work, please refer to our conference paper or watch the SIGCOMM presentation video.
Nirav Atre is a third-year PhD student in the Computer Science Department at Carnegie Mellon University studying networking and performance modelling.
The views expressed by the authors of this blog are their own and do not necessarily reflect the views of APNIC. Please note a Code of Conduct applies to this blog.
